Roth-Ruckenstein's factorization. More...

#include <RR_Factorization.h>

Collaboration diagram for rssoft::RR_Factorization:

Public Member Functions
	RR_Factorization (const gf::GFq &_gf, unsigned int _k)
	~RR_Factorization ()
void	init ()
void	set_verbosity (unsigned int _verbosity)
std::vector< gf::GFq_Polynomial > &	run (const gf::GFq_BivariatePolynomial &polynomial)
Protected Member Functions
gf::GFq_Polynomial	node_run (RR_Node &rr_node)
Protected Attributes
const gf::GFq &	gf
	Reference to the Galois Field being used.
unsigned int	k
	k as in RS(n,k)
unsigned int	verbosity
	verbosity level, 0 for none
unsigned int	t
	nodes but root node count
std::vector< gf::GFq_Polynomial >	F
	Result list of f(X) polynomials.

Detailed Description

Roth-Ruckenstein's factorization.

Constructor & Destructor Documentation

rssoft::RR_Factorization::RR_Factorization	(	const gf::GFq &	_gf,
		unsigned int	_k
	)

Constructor

Parameters:

gf	Reference to the Galois Field being used
k	as in RS(n,k)

                                                                    :
                gf(_gf),
                k(_k),
                t(0),
        verbosity(0)
{

}

rssoft::RR_Factorization::~RR_Factorization ( )

Destructor

{

}

Member Function Documentation

void rssoft::RR_Factorization::init ( )

Initialization before run

{
        t = 0;
        F.clear();
}

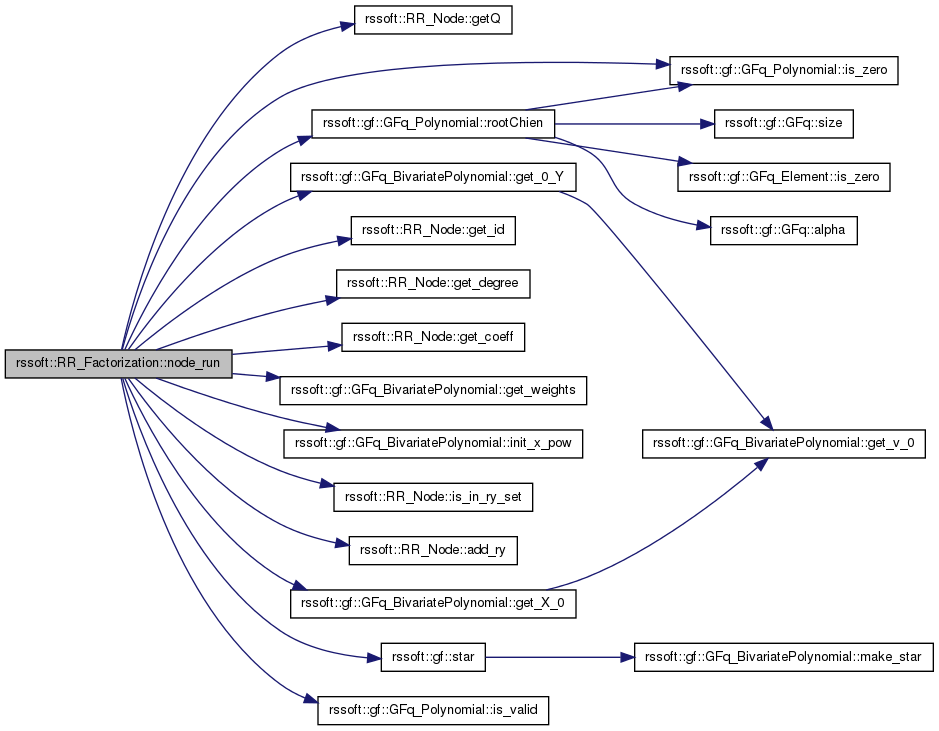
gf::GFq_Polynomial rssoft::RR_Factorization::node_run ( RR_Node & rr_node ) [protected]

Recursive run on a node

Parameters:

rr_node The node

Returns:: partial polynomial built at the node

{
        gf::GFq_BivariatePolynomial Qu = rr_node.getQ();
    gf::GFq_Polynomial Qy = Qu.get_0_Y();
        std::vector<rssoft::gf::GFq_Element> roots_y;
        Qy.rootChien(roots_y);
        std::vector<rssoft::gf::GFq_Element>::const_iterator ry_it = roots_y.begin();
    
    DEBUG_OUT(verbosity > 0, "*** Node #" << rr_node.get_id() << ": " << rr_node.get_degree() << " " << rr_node.get_coeff() << std::endl);
    
    if (ry_it != roots_y.end())
    {
        const gf::GFq& gf = ry_it->field();
        gf::GFq_BivariatePolynomial X1Y0(Qu.get_weights());
        X1Y0.init_x_pow(gf, 1); // X1Y0(X,Y) = X 
        rssoft::gf::GFq_BivariateMonomial m_XY(rssoft::gf::GFq_Element(gf,1),1,1); // X*Y
        std::vector<gf::GFq_Element> poly_X1;
        poly_X1.push_back(gf::GFq_Element(gf,0));
        poly_X1.push_back(gf::GFq_Element(gf,1));
        gf::GFq_Polynomial X1(gf, poly_X1); // X1(X) = X

        for (; ry_it != roots_y.end(); ++ry_it)
        {
            if (!rr_node.is_in_ry_set(*ry_it))
            {
                rr_node.add_ry(*ry_it);
                gf::GFq_BivariatePolynomial Yv(Qu.get_weights()); // Yv(X,Y) = X*Y + ry
                std::vector<rssoft::gf::GFq_BivariateMonomial> monos_Yv; 
                rssoft::gf::GFq_BivariateMonomial m_ry(*ry_it,0,0);
                monos_Yv.push_back(m_ry);
                monos_Yv.push_back(m_XY);
                Yv.init(monos_Yv);
                gf::GFq_BivariatePolynomial Qv = star(Qu(X1Y0,Yv));
                DEBUG_OUT(verbosity > 0, "    ry = " << *ry_it << " : Qv = " << Qv << std::endl);
                
                // Optimization: anticipate behaviour at child node
                bool Qv_for_Y_eq_0_is_0 = (Qv.get_X_0().is_zero()); // Qv(Y=0) = 0
                if (Qv_for_Y_eq_0_is_0) // Qv(Y=0) = 0
                {
                    if (rr_node.get_degree() < k-1)
                    { // trace back this route from node v
                        DEBUG_OUT(verbosity > 1, "    -> trace back this route from node v: " << (rr_node.get_coeff()*(X1^rr_node.get_degree()))+(*ry_it*(X1^(rr_node.get_degree()+1))) << std::endl);
                        return (rr_node.get_coeff()*(X1^rr_node.get_degree()))+(*ry_it*(X1^(rr_node.get_degree()+1))); 
                    }
                    else
                    { // trace back this route from node u
                        DEBUG_OUT(verbosity > 1, "    -> trace back this route from node u: " << rr_node.get_coeff()*(X1^rr_node.get_degree()) << std::endl);
                        return rr_node.get_coeff()*(X1^rr_node.get_degree()); 
                    }
                }
                else if ((rr_node.get_degree() == k-1) && !Qv_for_Y_eq_0_is_0)
                {
                        DEBUG_OUT(verbosity > 1, "    -> invalidate the route by returning an invalid polynomial" << std::endl);
                        return gf::GFq_Polynomial(gf); // invalidate the route by returning an invalid polynomial
                }
                                else
                                { // construct a child node
                                        t++;
                                        DEBUG_OUT(verbosity > 1, "    child #" << t << std::endl);
                                        RR_Node child_node(&rr_node, Qv, *ry_it, t);
                                        gf::GFq_Polynomial part_Fv = node_run(child_node); // Recursive call

                                        if (rr_node.get_degree() == -1) // we are at the root node
                                        {
                                                DEBUG_OUT(verbosity > 0, "    we are at root node" << std::endl);
                                                if (part_Fv.is_valid())
                                                {
                                                        DEBUG_OUT(verbosity > 0, "    Fi = " << part_Fv << std::endl);
                                                        F.push_back(part_Fv); // collect result
                                                }
                                        }
                                        else
                                        {
                                                if (!part_Fv.is_valid())
                                                {
                                                        DEBUG_OUT(verbosity > 1, "    -> propagate invalid route" << std::endl);
                                                        return part_Fv;
                                                }
                                                else
                                                {
                                                        DEBUG_OUT(verbosity > 1, "    -> return partial polynomial: " << ((rr_node.get_coeff()*(X1^rr_node.get_degree())) + part_Fv) <<  std::endl);
                                                        return (rr_node.get_coeff()*(X1^rr_node.get_degree())) + part_Fv;
                                                }
                                        }
                                }
            }
        }
    }

    return gf::GFq_Polynomial(gf);
}

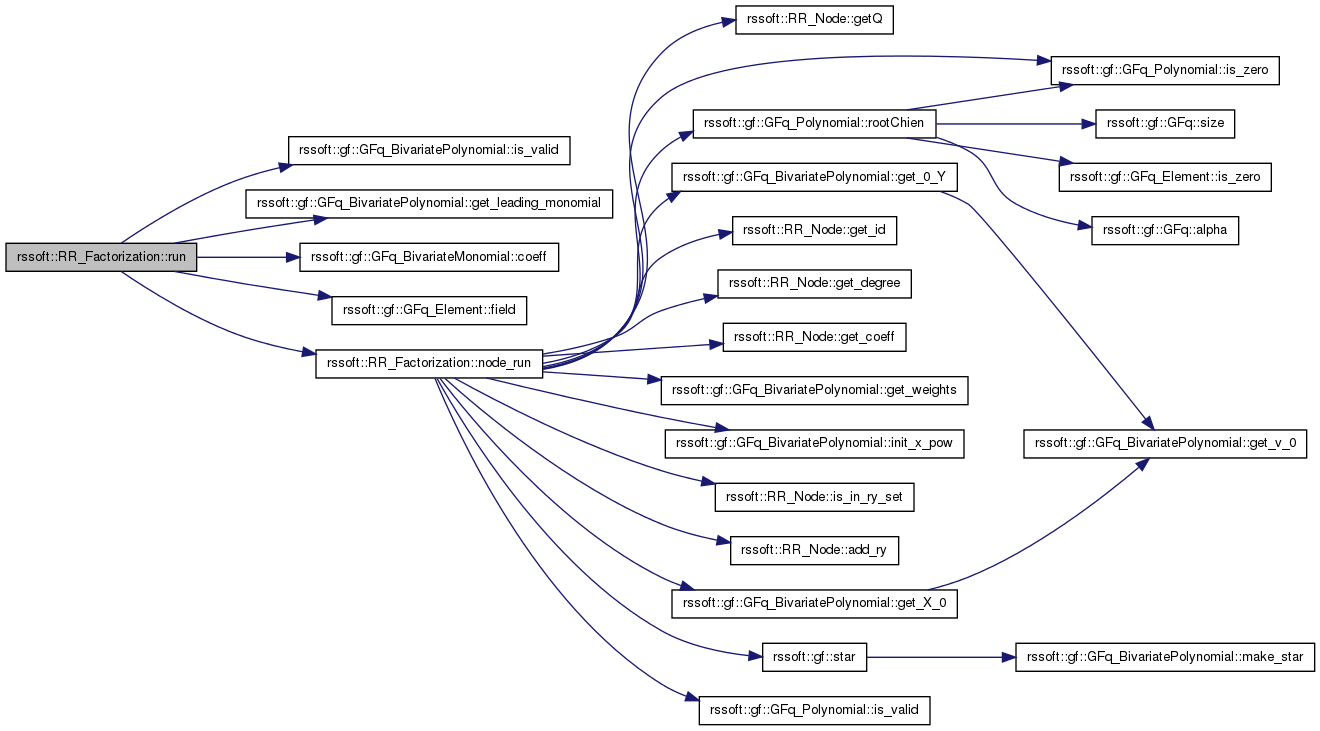
Here is the call graph for this function:

std::vector< gf::GFq_Polynomial > & rssoft::RR_Factorization::run ( const gf::GFq_BivariatePolynomial & polynomial )

Run factorization of given polynomial

Parameters:

polynomial Input polynomial

Returns:: list of polynomial factors

{
    if (!polynomial.is_valid())
    {
        throw RSSoft_Exception("Invalid polynomial");
    }
    else
    {
        const gf::GFq& gf = polynomial.get_leading_monomial().coeff().field();
        RR_Node u(0, polynomial, gf::GFq_Element(gf,0), t);
        node_run(u);
        return F;
    }
}

Here is the call graph for this function:

void rssoft::RR_Factorization::set_verbosity ( unsigned int _verbosity ) [inline]

Set verbosity level, 0 for none. This is active only in debug mode (CPPFLAGS=-D_DEBUG)

    {
        verbosity = _verbosity;
    }

Member Data Documentation

std::vector<gf::GFq_Polynomial> rssoft::RR_Factorization::F [protected]

Result list of f(X) polynomials.

const gf::GFq& rssoft::RR_Factorization::gf [protected]

Reference to the Galois Field being used.

unsigned int rssoft::RR_Factorization::k [protected]

k as in RS(n,k)

unsigned int rssoft::RR_Factorization::t [protected]

nodes but root node count

unsigned int rssoft::RR_Factorization::verbosity [protected]

verbosity level, 0 for none

The documentation for this class was generated from the following files:

/shared/development/google_code/rssoft/library/lib/RR_Factorization.h
/shared/development/google_code/rssoft/library/lib/RR_Factorization.cpp

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation