 |
rssoft
0.0.0
Reed-Solomon codes library with soft decision decoding
|
 |
rssoft
0.0.0
Reed-Solomon codes library with soft decision decoding
|
| typedef unsigned char rssoft::gf::GF2_Symbol |
External representation of symbol in GF(2)
| typedef std::pair<GFq_BivariateMonomialExponents, GFq_Element> rssoft::gf::GFq_BivariateMonomialKeyValueRepresentation |
Monomial representation as a (key, value) pair where key is the pair of exponents and value the coefficient It serves the purpose to be directly usable in the bivariate polynomial's map of monomials
| typedef int rssoft::gf::GFq_Symbol |
Symbol or binary-polynomial representation (ex: 5 is X^2+1)
| unsigned int rssoft::gf::binomial_coeff | ( | unsigned int | n, |
| unsigned int | k | ||
| ) |
| bool rssoft::gf::binomial_coeff_parity | ( | unsigned int | n, |
| unsigned int | k | ||
| ) |
Computes parity of a binomial coefficient
{
while (k>0)
{
if ((n%2 == 0) && (k%2 == 1))
{
return true;
}
n /= 2;
k /= 2;
}
return false; // k = 0
}
| unsigned int rssoft::gf::coeff_parity | ( | const GF2_Polynomial & | a | ) |
Gives the number of non null coefficients of a polynomial
| a | Polynomial |
{
const std::vector<GF2_Element>& poly = a.get_poly();
std::vector<GF2_Element>::const_iterator it = poly.begin();
unsigned int count=0;
for (; it != poly.end(); ++it)
{
if (*it != 0)
{
count++;
}
}
return count;
}

| bool rssoft::gf::compare_symbol_vectors | ( | const std::vector< GFq_Symbol > & | v1, |
| const std::vector< GFq_Symbol > & | v2 | ||
| ) |
{
if (v1.size() != v2.size())
{
return false;
}
for (unsigned int i=0; i<v1.size(); i++)
{
if (v1[i] != v2[i])
{
return false;
}
}
return true;
}
| GFq_BivariatePolynomial rssoft::gf::dHasse | ( | unsigned int | mu, |
| unsigned int | nu, | ||
| const GFq_BivariatePolynomial & | a | ||
| ) |
[mu,nu] Hasse derivative
| mu | mu parameter (applies to X factors) |
| nu | nu parameter (applies to Y factors) |
| a | Input polynomial |
{
GFq_BivariatePolynomial result(a);
result.make_dHasse(mu, nu);
return result;
}

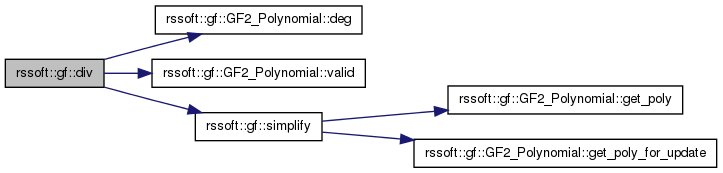
| std::pair< GF2_Polynomial, GF2_Polynomial > rssoft::gf::div | ( | const GF2_Polynomial & | a, |
| const GF2_Polynomial & | b | ||
| ) |
Long (or Euclidean) division returning both quotient and remainder
| a | Dividend |
| b | Divisor |
{
if (divisor.deg() < 0)
{
throw GF_Exception("GF Poly Division invalid operands");
}
else
{
if (divisor.deg() == 0)
{
GF2_Polynomial quotient(dividend);
quotient /= divisor[0];
return std::make_pair(quotient, GF2_Polynomial((GF2_Element)0));
}
else if (dividend.deg() < divisor.deg())
{
return std::make_pair(dividend, GF2_Polynomial((GF2_Element)0));
}
else
{
GF2_Polynomial remainder(dividend);
GF2_Polynomial quotient(dividend.deg() - divisor.deg() + 1, 0); // creates a polynomial with all zero coefficients
while (remainder.valid() && (remainder.deg() >= divisor.deg()))
{
quotient[remainder.deg() - divisor.deg()] = remainder[remainder.deg()] / divisor[divisor.deg()];
int r,d;
for (r=remainder.deg(), d=divisor.deg(); d >=0; r--, d--)
{
remainder[r] -= quotient[remainder.deg() - divisor.deg()]*divisor[d];
}
simplify(remainder);
}
simplify(quotient);
return std::make_pair(quotient, remainder);
}
}
}
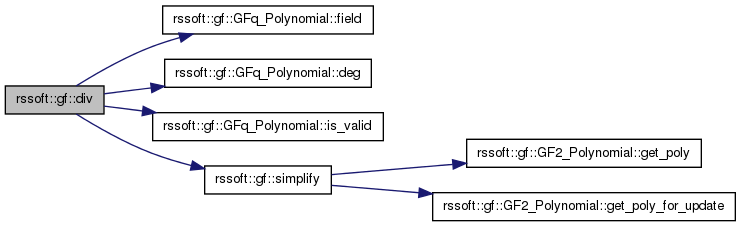
| std::pair< GFq_Polynomial, GFq_Polynomial > rssoft::gf::div | ( | const GFq_Polynomial & | a, |
| const GFq_Polynomial & | b | ||
| ) |
Long (or Euclidean) division returning both quotient and remainder
{
if ((dividend.field() != divisor.field()) || (divisor.deg() < 0))
{
throw GF_Exception("GFq Polynomial Division invalid operands");
}
else
{
if (divisor.deg() == 0)
{
GFq_Polynomial quotient(dividend);
quotient /= divisor[0];
return std::make_pair(quotient, GFq_Polynomial(quotient.field(), 0));
}
else if (dividend.deg() < divisor.deg())
{
return std::make_pair(dividend, GFq_Polynomial(dividend.field(), 0));
}
else
{
GFq_Polynomial remainder(dividend);
GFq_Polynomial quotient(dividend.field(), dividend.deg() - divisor.deg() + 1);
while (remainder.is_valid() && (remainder.deg() >= divisor.deg()))
{
quotient[remainder.deg() - divisor.deg()] = remainder[remainder.deg()] / divisor[divisor.deg()];
int r,d;
for (r=remainder.deg(), d=divisor.deg(); d >=0; r--, d--)
{
remainder[r] -= quotient[remainder.deg() - divisor.deg()]*divisor[d];
}
simplify(remainder);
}
simplify(quotient);
return std::make_pair(quotient, remainder);
}
}
}
| unsigned int rssoft::gf::factorial | ( | unsigned int | x, |
| unsigned int | result = 1 |
||
| ) |
Computes factorial
| n | input value |
{
if (x == 0)
{
return 1;
}
else if (x == 1)
{
return result;
}
else
{
return factorial(x - 1, x * result);
}
}
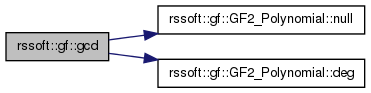
| GF2_Polynomial rssoft::gf::gcd | ( | const GF2_Polynomial & | a, |
| const GF2_Polynomial & | b | ||
| ) |
Get the Greatest Common Divisor of two polynomials. The order in which you enter them does not matter. It will make appropriate choices so gcd(a,b) and gcd(b,a) are equivalent. gcd(0,0) is invalid, gcd(a,0) yields a and gcd(0,b) yields b.
| a | Polynomial a |
| b | Polynomial b |
{
if (a.null() && b.null())
{
throw GF_Exception("GCD with both zero operand polynomials");
}
if (a.null())
{
return b;
}
if (b.null())
{
return a;
}
GF2_Polynomial r = ((a.deg() < b.deg()) ? a : b);
GF2_Polynomial x = ((a.deg() < b.deg()) ? b : a);
GF2_Polynomial t = ((a.deg() < b.deg()) ? b : a);
while (!r.null())
{
t = r;
r = x % t;
x = t;
}
return x;
}
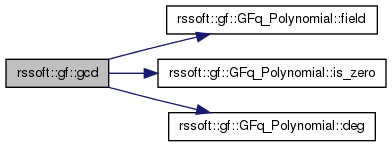
| GFq_Polynomial rssoft::gf::gcd | ( | const GFq_Polynomial & | a, |
| const GFq_Polynomial & | b | ||
| ) |
Get the Greatest Common Divisor of two polynomials. The order in which you enter them does not matter. It will make appropriate choices so gcd(a,b) and gcd(b,a) are equivalent. gcd(0,0) is invalid, gcd(a,0) yields a and gcd(0,b) yields b.
| a | Polynomial a |
| b | Polynomial b |
{
if ((a.field()) == (b.field()))
{
if (a.is_zero() && b.is_zero())
{
throw GF_Exception("GCD with both zero operand polynomials");
}
if (a.is_zero())
{
return b;
}
if (b.is_zero())
{
return a;
}
GFq_Polynomial r = ((a.deg() < b.deg()) ? a : b);
GFq_Polynomial x = ((a.deg() < b.deg()) ? b : a);
GFq_Polynomial t = ((a.deg() < b.deg()) ? b : a);
while (!r.is_zero())
{
t = r;
r = x % t;
x = t;
}
return x;
}
else
{
throw GF_Exception("GCD with unmatching Galois Fields for operand polynomials");
}
}
| GFq_Polynomial rssoft::gf::get_monic | ( | const GFq_Polynomial & | a, |
| GFq_Element & | lead_poly | ||
| ) |
Get the monic polynomial from a polynomial
| a | Polynomial to get monic from |
| lead_coeff | Reference to a GaloisFieldElement which will receive the original leading polynomial |
{
GFq_Polynomial result = a;
lead_poly = result.make_monic();
return result;
}

| GFq_Symbol rssoft::gf::gfq_element_to_symbol | ( | const GFq_Element & | gfe | ) |
{
return gfe.poly();
}

| bool rssoft::gf::irreducible | ( | const GF2_Polynomial & | a | ) |
Tells if the polynomial is irreducible
| a | Polynomial to test |
{
int df = f.deg();
// trivial answers
if (df <= 0)
{
return false;
}
else if (df == 1)
{
return true;
}
// real stuff...
else
{
rssoft::gf::GF2_Element Te[3] = {
rssoft::gf::GF2_Element(0),
rssoft::gf::GF2_Element(1),
rssoft::gf::GF2_Element(1),
};
size_t Te_sz = sizeof(Te)/sizeof(rssoft::gf::GF2_Element);
rssoft::gf::GF2_Polynomial T(Te_sz,Te); // T(x) = x^2 + x
rssoft::gf::GF2_Polynomial One(rssoft::gf::GF2_Element(1)); // One(x)=1
return (gcd(f,T) == One); // or gcd(f,(X2-X)%f) but for deg >= 2 this does not matter
}
}

| GFq_BivariateMonomialKeyValueRepresentation rssoft::gf::make_bivariate_monomial | ( | GFq_Element | coeff, |
| unsigned int | exp_x, | ||
| unsigned int | exp_y | ||
| ) |
Helper to create a monomial representation
{
return std::make_pair(std::make_pair(exp_x, exp_y), coeff);
}
| GF2_Polynomial rssoft::gf::operator% | ( | const GF2_Polynomial & | a, |
| const GF2_Polynomial & | b | ||
| ) |
{
GF2_Polynomial result = a;
result %= b;
return result;
}
| GF2_Polynomial rssoft::gf::operator% | ( | const GF2_Polynomial & | a, |
| const unsigned int & | power | ||
| ) |
{
GF2_Polynomial result = a;
result %= power;
return result;
}
| GFq_Polynomial rssoft::gf::operator% | ( | const GFq_Polynomial & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
GFq_Polynomial result = a;
result %= b;
return result;
}
| GFq_Polynomial rssoft::gf::operator% | ( | const GFq_Polynomial & | a, |
| const unsigned int & | power | ||
| ) |
{
GFq_Polynomial result = a;
result %= power;
return result;
}
| GF2_Element rssoft::gf::operator* | ( | const GF2_Element & | a, |
| const GF2_Element & | b | ||
| ) |
{
GF2_Element result = a;
result *= b;
return result;
}
| GF2_Element rssoft::gf::operator* | ( | const GF2_Element & | a, |
| const GF2_Symbol & | b | ||
| ) |
{
GF2_Element result = a;
result *= b;
return result;
}
| GF2_Element rssoft::gf::operator* | ( | const GF2_Symbol & | a, |
| const GF2_Element & | b | ||
| ) |
{
GF2_Element result = b;
result *= a;
return result;
}
| GFq_Element rssoft::gf::operator* | ( | const GFq_Element & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_Element result = a;
result *= b;
return result;
}
| GFq_Element rssoft::gf::operator* | ( | const GFq_Element & | a, |
| const GFq_Symbol & | b | ||
| ) |
{
GFq_Element result = a;
result *= b;
return result;
}
| GFq_Element rssoft::gf::operator* | ( | const GFq_Symbol & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_Element result = b;
result *= a;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator* | ( | const GFq_BivariateMonomial & | a, |
| const GFq_BivariateMonomial & | b | ||
| ) |
{
GFq_BivariateMonomial result(a);
result *= b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator* | ( | const GFq_BivariateMonomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_BivariateMonomial result(a);
result *= b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator* | ( | const GFq_Element & | a, |
| const GFq_BivariateMonomial & | b | ||
| ) |
{
GFq_BivariateMonomial result(b);
result *= a;
return result;
}
| GF2_Polynomial rssoft::gf::operator* | ( | const GF2_Polynomial & | a, |
| const GF2_Polynomial & | b | ||
| ) |
{
GF2_Polynomial result = a;
result *= b;
return result;
}
| GF2_Polynomial rssoft::gf::operator* | ( | const GF2_Element & | a, |
| const GF2_Polynomial & | b | ||
| ) |
{
GF2_Polynomial result = b;
result *= a;
return result;
}
| GF2_Polynomial rssoft::gf::operator* | ( | const GF2_Polynomial & | a, |
| const GF2_Element & | b | ||
| ) |
{
GF2_Polynomial result = a;
result *= b;
return result;
}
| GFq_Polynomial rssoft::gf::operator* | ( | const GFq_Polynomial & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
GFq_Polynomial result = a;
result *= b;
return result;
}
| GFq_Polynomial rssoft::gf::operator* | ( | const GFq_Element & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
GFq_Polynomial result = b;
result *= a;
return result;
}
| GFq_Polynomial rssoft::gf::operator* | ( | const GFq_Polynomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_Polynomial result = a;
result *= b;
return result;
}
| GFq_BivariatePolynomial rssoft::gf::operator* | ( | const GFq_BivariatePolynomial & | a, |
| const GFq_BivariatePolynomial & | b | ||
| ) |
{
GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(a.get_weights());
std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> product_monomials(mono_exp_compare);
GFq_BivariatePolynomial result(a.get_weights()); // copy without creating monomials
GFq_BivariatePolynomial::product(product_monomials, a, b);
result.init(product_monomials);
return result;
}

| GFq_BivariatePolynomial rssoft::gf::operator* | ( | const GFq_BivariatePolynomial & | a, |
| const GFq_BivariateMonomial & | b | ||
| ) |
{
GFq_BivariatePolynomial result(a);
result *= b;
return result;
}
| GFq_BivariatePolynomial rssoft::gf::operator* | ( | const GFq_BivariatePolynomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_BivariatePolynomial result(a);
result *= b;
return result;
}
| GFq_BivariatePolynomial rssoft::gf::operator* | ( | const GFq_Element & | a, |
| const GFq_BivariatePolynomial & | b | ||
| ) |
{
GFq_BivariatePolynomial result(b);
result *= a;
return result;
}
| GF2_Element rssoft::gf::operator+ | ( | const GF2_Element & | a, |
| const GF2_Element & | b | ||
| ) |
{
GF2_Element result = a;
result += b;
return result;
}
| GFq_Element rssoft::gf::operator+ | ( | const GFq_Element & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_Element result = a;
result += b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator+ | ( | const GFq_BivariateMonomial & | a, |
| const GFq_BivariateMonomial & | b | ||
| ) |
{
GFq_BivariateMonomial result(a);
result += b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator+ | ( | const GFq_BivariateMonomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_BivariateMonomial result(a);
result += b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator+ | ( | const GFq_Element & | a, |
| const GFq_BivariateMonomial & | b | ||
| ) |
{
GFq_BivariateMonomial result(b);
result += a;
return result;
}
| GF2_Polynomial rssoft::gf::operator+ | ( | const GF2_Polynomial & | a, |
| const GF2_Polynomial & | b | ||
| ) |
{
GF2_Polynomial result = a;
result += b;
return result;
}
| GF2_Polynomial rssoft::gf::operator+ | ( | const GF2_Polynomial & | a, |
| const GF2_Element & | b | ||
| ) |
{
GF2_Polynomial result = a;
result += b;
return result;
}
| GF2_Polynomial rssoft::gf::operator+ | ( | const GF2_Element & | a, |
| const GF2_Polynomial & | b | ||
| ) |
{
GF2_Polynomial result = b;
result += a;
return result;
}
| GFq_Polynomial rssoft::gf::operator+ | ( | const GFq_Polynomial & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
GFq_Polynomial result = a;
result += b;
return result;
}
| GFq_Polynomial rssoft::gf::operator+ | ( | const GFq_Polynomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_Polynomial result = a;
result += b;
return result;
}
| GFq_Polynomial rssoft::gf::operator+ | ( | const GFq_Element & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
GFq_Polynomial result = b;
result += a;
return result;
}
| GFq_Polynomial rssoft::gf::operator+ | ( | const GFq_Polynomial & | a, |
| const GFq_Symbol & | b | ||
| ) |
{
return a + GFq_Element(a.field(), b);
}

| GFq_Polynomial rssoft::gf::operator+ | ( | const GFq_Symbol & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
return b + GFq_Element(b.field(), a);
}

| GFq_BivariatePolynomial rssoft::gf::operator+ | ( | const GFq_BivariatePolynomial & | a, |
| const GFq_BivariatePolynomial & | b | ||
| ) |
{
GFq_BivariatePolynomial result(a.get_weights()); // copy without creating monomials
std::vector<GFq_BivariateMonomial> sum_monomials;
GFq_BivariatePolynomial::sum(sum_monomials, a, b);
result.init(sum_monomials);
return result;
}

| GFq_BivariatePolynomial rssoft::gf::operator+ | ( | const GFq_BivariatePolynomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_BivariatePolynomial result(a);
result += b;
return result;
}
| GFq_BivariatePolynomial rssoft::gf::operator+ | ( | const GFq_Element & | a, |
| const GFq_BivariatePolynomial & | b | ||
| ) |
{
GFq_BivariatePolynomial result(b);
result += a;
return result;
}
| GF2_Element rssoft::gf::operator- | ( | const GF2_Element & | a, |
| const GF2_Element & | b | ||
| ) |
{
GF2_Element result = a;
result -= b;
return result;
}
| GFq_Element rssoft::gf::operator- | ( | const GFq_Element & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_Element result = a;
result -= b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator- | ( | const GFq_BivariateMonomial & | a, |
| const GFq_BivariateMonomial & | b | ||
| ) |
{
GFq_BivariateMonomial result(a);
result -= b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator- | ( | const GFq_BivariateMonomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_BivariateMonomial result(a);
result -= b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator- | ( | const GFq_Element & | a, |
| const GFq_BivariateMonomial & | b | ||
| ) |
{
GFq_BivariateMonomial result(b);
result -= a;
return result;
}
| GF2_Polynomial rssoft::gf::operator- | ( | const GF2_Polynomial & | a, |
| const GF2_Polynomial & | b | ||
| ) |
{
GF2_Polynomial result = a;
result -= b;
return result;
}
| GF2_Polynomial rssoft::gf::operator- | ( | const GF2_Polynomial & | a, |
| const GF2_Element & | b | ||
| ) |
{
GF2_Polynomial result = a;
result -= b;
return result;
}
| GF2_Polynomial rssoft::gf::operator- | ( | const GF2_Element & | a, |
| const GF2_Polynomial & | b | ||
| ) |
{
GF2_Polynomial result = b;
result -= a;
return result;
}
| GFq_Polynomial rssoft::gf::operator- | ( | const GFq_Polynomial & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
GFq_Polynomial result = a;
result -= b;
return result;
}
| GFq_Polynomial rssoft::gf::operator- | ( | const GFq_Polynomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_Polynomial result = a;
result -= b;
return result;
}
| GFq_Polynomial rssoft::gf::operator- | ( | const GFq_Element & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
GFq_Polynomial result = b;
result -= a;
return result;
}
| GFq_Polynomial rssoft::gf::operator- | ( | const GFq_Polynomial & | a, |
| const GFq_Symbol & | b | ||
| ) |
{
return a - GFq_Element(a.field(), b);
}

| GFq_Polynomial rssoft::gf::operator- | ( | const GFq_Symbol & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
return b - GFq_Element(b.field(), a);
}

| GFq_BivariatePolynomial rssoft::gf::operator- | ( | const GFq_BivariatePolynomial & | a, |
| const GFq_BivariatePolynomial & | b | ||
| ) |
{
return a+b;
}
| GFq_BivariatePolynomial rssoft::gf::operator- | ( | const GFq_BivariatePolynomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
return a+b;
}
| GFq_BivariatePolynomial rssoft::gf::operator- | ( | const GFq_Element & | a, |
| const GFq_BivariatePolynomial & | b | ||
| ) |
{
return a+b;
}
| GF2_Element rssoft::gf::operator/ | ( | const GF2_Element & | a, |
| const GF2_Element & | b | ||
| ) |
{
GF2_Element result = a;
result /= b;
return result;
}
| GFq_Element rssoft::gf::operator/ | ( | const GFq_Element & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_Element result = a;
result /= b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator/ | ( | const GFq_BivariateMonomial & | a, |
| const GFq_BivariateMonomial & | b | ||
| ) |
{
GFq_BivariateMonomial result(a);
result /= b;
return result;
}
| GFq_BivariateMonomial rssoft::gf::operator/ | ( | const GFq_BivariateMonomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_BivariateMonomial result(a);
result /= b;
return result;
}
| GF2_Polynomial rssoft::gf::operator/ | ( | const GF2_Polynomial & | a, |
| const GF2_Polynomial & | b | ||
| ) |
{
GF2_Polynomial result = a;
result /= b;
return result;
}
| GF2_Polynomial rssoft::gf::operator/ | ( | const GF2_Polynomial & | a, |
| const GF2_Element & | b | ||
| ) |
{
GF2_Polynomial result = a;
result /= b;
return result;
}
| GFq_Polynomial rssoft::gf::operator/ | ( | const GFq_Polynomial & | a, |
| const GFq_Polynomial & | b | ||
| ) |
{
GFq_Polynomial result = a;
result /= b;
return result;
}
| GFq_Polynomial rssoft::gf::operator/ | ( | const GFq_Polynomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_Polynomial result = a;
result /= b;
return result;
}
| GFq_BivariatePolynomial rssoft::gf::operator/ | ( | const GFq_BivariatePolynomial & | a, |
| const GFq_BivariateMonomial & | b | ||
| ) |
{
GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(a.get_weights());
std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> div_monomials(mono_exp_compare);
GFq_BivariatePolynomial result(a.get_weights()); // copy without creating monomials
GFq_BivariatePolynomial::division(div_monomials, a, b);
result.init(div_monomials);
return result;
}

| GFq_BivariatePolynomial rssoft::gf::operator/ | ( | const GFq_BivariatePolynomial & | a, |
| const GFq_Element & | b | ||
| ) |
{
GFq_BivariatePolynomial result(a);
result /= b;
return result;
}
| std::ostream& rssoft::gf::operator<< | ( | std::ostream & | os, |
| const GF2_Element & | gfe | ||
| ) |
{
os << (gfe.bin_value ? 1 : 0);
return os;
}
| std::ostream& rssoft::gf::operator<< | ( | std::ostream & | os, |
| const GFq_Element & | gfe | ||
| ) |
{
//os << gfe.poly_value;
if (gfe.poly_value == 0)
{
os << "0";
}
else if (gfe.poly_value == 1)
{
os << "1";
}
else
{
os << "a^" << gfe.field().index(gfe.poly_value);
}
return os;
}
| std::ostream & rssoft::gf::operator<< | ( | std::ostream & | os, |
| const GFq_BivariateMonomialKeyValueRepresentation & | monomial | ||
| ) |
Prints monomials to output stream
{
if (monomial.first.are_zero())
{
os << monomial.second;
}
else
{
if (monomial.second != 1)
{
os << monomial.second;
os << "*";
}
}
if (monomial.first.x() > 0)
{
os << "X";
if (monomial.first.x() > 1)
{
os << "^" << monomial.first.x();
}
if (monomial.first.y() > 0)
{
os << "*";
}
}
if (monomial.first.y() > 0)
{
os << "Y";
if (monomial.first.y() > 1)
{
os << "^" << monomial.first.y();
}
}
return os;
}
| std::ostream& rssoft::gf::operator<< | ( | std::ostream & | os, |
| const GFq & | gf | ||
| ) |
{
os << "GF(2^" << gf.pwr() << ")" << std::endl;
os << "P = " << gf.primitive_poly << std::endl;
os << "i\ta^i\tlog_a(i)" << std::endl;
for(unsigned int i = 0; i < gf.field_size + 1; i++)
{
os << i << "\t" << gf.alpha_to[i] << "\t" << gf.index_of[i] << std::endl;
}
return os;
}

| GF2_Polynomial rssoft::gf::operator<< | ( | const GF2_Polynomial & | a, |
| const unsigned int & | n | ||
| ) |
Shifts coefficients up by n. This increases the degree by n. Lower positions are filled with zero coefficients.
{
GF2_Polynomial result = a;
result <<= n;
return result;
}
| std::ostream& rssoft::gf::operator<< | ( | std::ostream & | os, |
| const GF2_Polynomial & | polynomial | ||
| ) |
Prints a polynomial to an output stream
{
if (polynomial.deg() >= 0)
{
bool is_null = true;
bool first_coeff = true;
for (unsigned int i = 0; i < polynomial.poly.size(); i++)
{
GF2_Element coeff = polynomial.poly[i];
if (coeff != 0)
{
is_null = false;
os << ((!first_coeff) ? "+ " : "");
if (i == 0)
{
os << "1 ";
}
else if (i==1)
{
os << "x ";
}
else
{
os << "x^" << i << " ";
}
first_coeff = false;
}
}
if (is_null)
{
os << "0";
}
}
return os;
}

| GFq_Polynomial rssoft::gf::operator<< | ( | const GFq_Polynomial & | a, |
| const unsigned int & | n | ||
| ) |
Shifts coefficients up by n. This increases the degree by n. Lower positions are filled with zero coefficients.
{
GFq_Polynomial result = a;
result <<= n;
return result;
}
| std::ostream& rssoft::gf::operator<< | ( | std::ostream & | os, |
| const GFq_Polynomial & | polynomial | ||
| ) |
Prints a polynomial to an output stream
{
if (polynomial.deg() >= 0)
{
bool is_null = true;
bool first_coeff = true;
for (unsigned int i = 0; i < polynomial.poly.size(); i++)
{
GFq_Symbol coeff = polynomial.poly[i].poly();
if (coeff != 0)
{
is_null = false;
os << ((!first_coeff) ? "+ " : "");
if (polynomial.alpha_format)
{
GFq_Symbol log_alpha = polynomial.poly[i].index();
if (log_alpha == 0)
{
if (i == 0)
{
os << "1 ";
}
else
{
os << "";
}
}
else if (log_alpha == 1)
{
os << "a" << ((!first_coeff) ? "*" : " ");
}
else
{
os << "a^" << log_alpha << ((!first_coeff) ? "*" : " ");
}
}
else
{
if (coeff == 1)
{
if (i != 0)
{
os << "";
}
else
{
os << coeff << " ";
}
}
else
{
os << coeff << ((!first_coeff) ? "*" : " ");
}
}
if (i != 0)
{
if (i == 1)
{
os << "X ";
}
else
{
os << "X^" << i << " ";
}
}
first_coeff = false;
}
}
if (is_null)
{
os << "0";
}
}
return os;
}

| std::ostream& rssoft::gf::operator<< | ( | std::ostream & | os, |
| const GFq_BivariatePolynomial & | polynomial | ||
| ) |
Prints a polynomial to an output stream
{
if (polynomial.monomials.size() == 0)
{
os << "<invalid>";
}
else
{
std::map<GFq_BivariateMonomialExponents, GFq_Element>::const_iterator it = polynomial.monomials.begin();
for (; it != polynomial.monomials.end(); ++it)
{
if (it != polynomial.monomials.begin())
{
os << " + ";
}
os << *it;
}
}
return os;
}
| GF2_Polynomial rssoft::gf::operator>> | ( | const GF2_Polynomial & | a, |
| const unsigned int & | n | ||
| ) |
Shifts coefficients up down n. This decreases the degree by n. if n is larger than the polynomial degree this will effectively create an invalid polynomial (without coefficients).
{
GF2_Polynomial result = a;
result >>= n;
return result;
}
| GFq_Polynomial rssoft::gf::operator>> | ( | const GFq_Polynomial & | a, |
| const unsigned int & | n | ||
| ) |
Shifts coefficients up down n. This decreases the degree by n. if n is larger than the polynomial degree this will effectively create an invalid polynomial (without coefficients).
{
GFq_Polynomial result = a;
result >>= n;
return result;
}
| GF2_Element rssoft::gf::operator^ | ( | const GF2_Element & | a, |
| const int & | b | ||
| ) |
{
GF2_Element result = a;
result ^= b;
return result;
}
| GFq_Element rssoft::gf::operator^ | ( | const GFq_Element & | a, |
| const int & | b | ||
| ) |
{
GFq_Element result = a;
result ^= b;
return result;
}
| GF2_Polynomial rssoft::gf::operator^ | ( | const GF2_Polynomial & | a, |
| const int & | n | ||
| ) |
{
GF2_Polynomial result = a;
result ^= n;
return result;
}
| GFq_Polynomial rssoft::gf::operator^ | ( | const GFq_Polynomial & | a, |
| const int & | n | ||
| ) |
{
GFq_Polynomial result = a;
result ^= n;
return result;
}
| GFq_BivariatePolynomial rssoft::gf::operator^ | ( | const GFq_BivariatePolynomial & | a, |
| unsigned int | n | ||
| ) |
{
GFq_BivariatePolynomial result(a);
result ^= n;
return result;
}
| bool rssoft::gf::primitive | ( | const GF2_Polynomial & | a, |
| unsigned int | m | ||
| ) |
Tells if the polynomial is primitive in GF(2^m). Uses heuristics and can serve to eliminate most non primitive polynomials however to build a GF(2^m) field it is recommended to use well known primitive polynomials
| a | Polynomial to test |
| m | m as in GF(2^m) |
{
unsigned int k = 1;
k <<= m;
k--; // 2^m-1
rssoft::gf::GF2_Polynomial One(rssoft::gf::GF2_Element(1)); // One(x)=1
rssoft::gf::GF2_Polynomial Xk(k); // Xk(x) = x^k
if (irreducible(a) && (a.deg() == m) && ((coeff_parity(a)%2)==1))
{
if (((Xk+One)%a).null())
{
return true;
}
else
{
return false;
}
}
else
{
return false;
}
}

| void rssoft::gf::print_elements_vector | ( | std::ostream & | os, |
| const std::vector< GFq_Element > & | v | ||
| ) |
{
std::vector<rssoft::gf::GFq_Element>::const_iterator c_it = v.begin();
os << "[";
for (; c_it != v.end(); ++c_it)
{
if (c_it != v.begin())
{
os << ", ";
}
os << *c_it;
}
os << "]";
}
| void rssoft::gf::print_symbols_and_erasures | ( | std::ostream & | os, |
| const std::vector< GFq_Symbol > & | v, | ||
| std::set< unsigned int > & | erasure_indexes | ||
| ) |
{
std::vector<rssoft::gf::GFq_Symbol>::const_iterator c_it = v.begin();
unsigned int i_c = 0;
os << "[";
for (; c_it != v.end(); ++c_it, i_c++)
{
if (c_it != v.begin())
{
os << ", ";
}
if (erasure_indexes.find(i_c) == erasure_indexes.end())
{
os << *c_it;
}
else
{
os << "*";
}
}
os << "]";
}
| void rssoft::gf::print_symbols_vector | ( | std::ostream & | os, |
| const std::vector< GFq_Symbol > & | v | ||
| ) |
{
std::vector<rssoft::gf::GFq_Symbol>::const_iterator c_it = v.begin();
os << "[";
for (; c_it != v.end(); ++c_it)
{
if (c_it != v.begin())
{
os << ", ";
}
os << *c_it;
}
os << "]";
}
| std::vector< GFq_Element > rssoft::gf::rootex | ( | const GFq_Polynomial & | a | ) |
Find roots of polynomial by exhaustive search
| a | Polynomial which roots are searched |
{
std::vector<GFq_Element> roots;
const GFq& gf = a.field();
for (unsigned int i=0; i<gf.size()+1; i++)
{
if (a(i) == 0)
{
roots.push_back(GFq_Element(gf,i));
}
}
return roots;
}
| std::vector< GFq_Element > rssoft::gf::rootex_nz | ( | const GFq_Polynomial & | a | ) |
Find non null roots of polynomial by exhaustive search
| a | Polynomial which roots are searched |
{
std::vector<GFq_Element> roots;
const GFq& gf = a.field();
for (unsigned int i=0; i<gf.size(); i++)
{
if (a(gf.alpha(i)) == 0)
{
roots.push_back(GFq_Element(gf,gf.alpha(i)));
}
}
return roots;
}
| void rssoft::gf::simplify | ( | GF2_Polynomial & | polynomial | ) |
{
if (polynomial.get_poly().size() > 0)
{
for (size_t i = polynomial.get_poly().size() - 1; i > 0; i--)
{
if (polynomial.get_poly()[i] == 0)
{
polynomial.get_poly_for_update().pop_back();
}
else
{
break;
}
}
}
}

| void rssoft::gf::simplify | ( | GFq_Polynomial & | polynomial | ) |
{
if (polynomial.get_poly().size() > 0)
{
for (size_t i = polynomial.get_poly().size() - 1; i > 0; i--)
{
if (polynomial.get_poly()[i] == 0)
{
polynomial.get_poly_for_update().pop_back();
}
else
{
break;
}
}
}
}

| void rssoft::gf::simplify | ( | GFq_BivariatePolynomial & | polynomial | ) |
Removes monomials with zero coefficients
{
std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>& monomials = polynomial.get_monomials_for_update();
GFq_BivariatePolynomial::simplify(monomials);
}

| std::vector< GFq_Polynomial > rssoft::gf::square_free_decomposition | ( | const GFq_Polynomial & | a | ) |
Square free decomposition of a polynomial using Yun's algorithm WARNING: largely untested and not validated
| a | Polynomial from which to do the square free decomposition |
{
const GFq& gf = ff.field();
GFq_Polynomial f = ff;
std::vector<GFq_Polynomial> hv;
unsigned int i = 1;
GFq_Polynomial u = gcd(f,f.derivative());
GFq_Polynomial v = f/u;
GFq_Polynomial w = f.derivative()/u;
while (!v.is_one())
{
GFq_Polynomial h = gcd(v, w-v.derivative());
v = v/h;
w = (w-v.derivative())/h;
hv.push_back(h);
i++;
}
return hv;
}
| GFq_BivariatePolynomial rssoft::gf::star | ( | const GFq_BivariatePolynomial & | a | ) |
Star function as P*(X,Y) = P(X,Y)/X^h where h is the greatest power of X so that X^h divides P
| a | Input polynomial |
{
GFq_BivariatePolynomial result(a);
result.make_star();
return result;
}

| const GFq_Symbol rssoft::gf::GFERROR = -1 |
Undefined symbol.