rssoft  0.0.0
Reed-Solomon codes library with soft decision decoding
Public Member Functions | Private Member Functions | Private Attributes | Friends
rssoft::gf::GFq Class Reference

Galois Field GF(q=2^m) class. Generates and holds lookup tables (LUT) for basic operations. Hosts basic operations and element representation conversions. More...

#include <GFq.h>

Collaboration diagram for rssoft::gf::GFq:
Collaboration graph
[legend]

List of all members.

Public Member Functions

 GFq (const int pwr, const GF2_Polynomial &primitive_poly)
 GFq (const GFq &gf)
 ~GFq ()
GFq & operator= (const GFq &gf)
bool operator== (const GFq &gf) const
bool operator!= (const GFq &gf) const
unsigned int index (const GFq_Symbol value) const
GFq_Symbol alpha (const unsigned int power) const
unsigned int size () const
unsigned int pwr () const
GFq_Symbol add (const GFq_Symbol &a, const GFq_Symbol &b) const
GFq_Symbol sub (const GFq_Symbol &a, const GFq_Symbol &b) const
GFq_Symbol mul (const GFq_Symbol &a, const GFq_Symbol &b) const
GFq_Symbol div (const GFq_Symbol &a, const GFq_Symbol &b) const
GFq_Symbol exp (const GFq_Symbol &a, const int &n) const
GFq_Symbol inverse (const GFq_Symbol &val) const

Private Member Functions

void generate_field ()
GFq_Symbol fast_modulus (GFq_Symbol x) const
GFq_Symbol gen_mul (const GFq_Symbol &a, const GFq_Symbol &b) const
GFq_Symbol gen_div (const GFq_Symbol &a, const GFq_Symbol &b) const
GFq_Symbol gen_exp (const GFq_Symbol &a, const unsigned int &n) const
GFq_Symbol gen_inverse (const GFq_Symbol &val) const

Private Attributes

unsigned int power
 m the power of 2 as in GF(2^m)
unsigned int field_size
 Number of non null elements in the field.
const GF2_Polynomial & primitive_poly
 Primitive polynomial.
unsigned int prim_poly_hash
 Primitive polynomial hash coded.
GFq_Symbol * alpha_to
 Exponential or anti-log unary operation LUT.
GFq_Symbol * index_of
 Log unary operation LUT.
GFq_Symbol * mul_inverse
 Multiplicative inverse unary operation LUT.
GFq_Symbol ** mul_table
 Multiplication binary operation LUT.
GFq_Symbol ** div_table
 Division binary operation LUT.
GFq_Symbol ** exp_table
 Exponent binary operation LUT.

Friends

std::ostream & operator<< (std::ostream &os, const GFq &gf)

Detailed Description

Galois Field GF(q=2^m) class. Generates and holds lookup tables (LUT) for basic operations. Hosts basic operations and element representation conversions.

Constructor & Destructor Documentation

rssoft::gf::GFq::GFq ( const int  pwr,
const GF2_Polynomial &  primitive_poly 
) 
                                                             :
                power(pwr), field_size((1 << power) - 1), primitive_poly(_primitive_poly)
{
        if (primitive(primitive_poly, pwr))
        {
                        alpha_to = new GFq_Symbol[field_size + 1];
                        index_of = new GFq_Symbol[field_size + 1];

                #if !defined(NO_GFLUT)

                        mul_table = new GFq_Symbol*[(field_size + 1)];
                        div_table = new GFq_Symbol*[(field_size + 1)];
                        exp_table = new GFq_Symbol*[(field_size + 1)];
                        mul_inverse = new GFq_Symbol[(field_size + 1) * 2];

                        for (unsigned int i = 0; i < (field_size + 1); i++)
                        {
                                mul_table[i] = new GFq_Symbol[(field_size + 1)];
                                div_table[i] = new GFq_Symbol[(field_size + 1)];
                                exp_table[i] = new GFq_Symbol[(field_size + 1)];
                        }

                #else

                        mul_table = new GFq_Symbol *[1];
                        div_table = new GFq_Symbol *[1];
                        exp_table = new GFq_Symbol *[1];
                        mul_inverse = new GFq_Symbol [1];

                #endif

                        prim_poly_hash = 0xAAAAAAAA;
                        unsigned int prim_poly_mono_power = 1;

                        for (unsigned int i = 0; i <= power; i++)
                        {
                                if (i < power)
                                {
                                        prim_poly_hash += ((i & 1) == 0) ? (  (prim_poly_hash <<  7) ^ primitive_poly[i].uint_value() ^ (prim_poly_hash >> 3)) :
                                                                          (~((prim_poly_hash << 11) ^ primitive_poly[i].uint_value() ^ (prim_poly_hash >> 5)));
                                }

                                prim_poly_mono_power <<= 1;
                        }

                        generate_field();
        }
        else
        {
                throw GF_Exception("Non primitive polynomial used to create GF(q) field");
        }
}

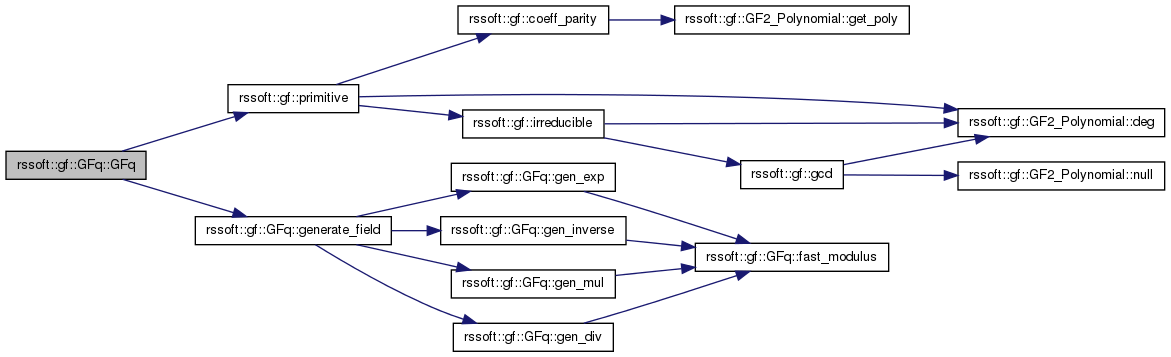
Here is the call graph for this function:

rssoft::gf::GFq::GFq ( const GFq &  gf) 
                      :
                primitive_poly(gf.primitive_poly)
{
        power = gf.power;
        field_size = gf.field_size;
        prim_poly_hash = gf.prim_poly_hash;
        alpha_to = new GFq_Symbol[field_size + 1];
        index_of = new GFq_Symbol[field_size + 1];

        memcpy(alpha_to, gf.alpha_to, (field_size + 1) * sizeof(GFq_Symbol));
        memcpy(index_of, gf.index_of, (field_size + 1) * sizeof(GFq_Symbol));

#if !defined(NO_GFLUT)

        mul_table = new GFq_Symbol*[(field_size + 1)];
        div_table = new GFq_Symbol*[(field_size + 1)];
        exp_table = new GFq_Symbol*[(field_size + 1)];
        mul_inverse = new GFq_Symbol[(field_size + 1) * 2];

        for (unsigned int i = 0; i < (field_size + 1); i++)
        {
                mul_table[i] = new GFq_Symbol[(field_size + 1)];
                div_table[i] = new GFq_Symbol[(field_size + 1)];
                exp_table[i] = new GFq_Symbol[(field_size + 1)];
        }

        memcpy(mul_inverse, gf.mul_inverse, (field_size + 1) * sizeof(GFq_Symbol) * 2);

        memcpy(mul_table, gf.mul_table, (field_size + 1) * sizeof(GFq_Symbol*));
        memcpy(div_table, gf.div_table, (field_size + 1) * sizeof(GFq_Symbol*));
        memcpy(exp_table, gf.exp_table, (field_size + 1) * sizeof(GFq_Symbol*));

        for (unsigned int i = 0; i < (field_size + 1); i++)
        {
                memcpy(mul_table[i], gf.mul_table[i], (field_size + 1) * sizeof(GFq_Symbol));
                memcpy(div_table[i], gf.div_table[i], (field_size + 1) * sizeof(GFq_Symbol));
                memcpy(exp_table[i], gf.exp_table[i], (field_size + 1) * sizeof(GFq_Symbol));
        }

#endif
}
rssoft::gf::GFq::~GFq ( ) 
{
        if (alpha_to != NULL)
        {
                delete[] alpha_to;
        }
        if (index_of != NULL)
        {
                delete[] index_of;
        }

#if !defined(NO_GFLUT)

        for (unsigned int i = 0; i < (field_size + 1); i++)
        {
                if (mul_table[i] != NULL)
                {
                        delete[] mul_table[i];
                }
                if (div_table[i] != NULL)
                {
                        delete[] div_table[i];
                }
                if (exp_table[i] != NULL)
                {
                        delete[] exp_table[i];
                }
        }

        if (mul_table != NULL)
        {
                delete[] mul_table;
        }

        if (div_table != NULL)
        {
                delete[] div_table;
        }

        if (exp_table != NULL)
        {
                delete[] exp_table;
        }

        if (mul_inverse != NULL)
        {
                delete[] mul_inverse;
        }

#endif
}

Member Function Documentation

GFq_Symbol rssoft::gf::GFq::add ( const GFq_Symbol &  a,
const GFq_Symbol &  b 
) const [inline] 
        {
                return (a ^ b);
        }
GFq_Symbol rssoft::gf::GFq::alpha ( const unsigned int  power) const [inline]

Alpha exponentiation

Parameters:
valueThe power of alpha
Returns:
The symbol representation to alpha raised to the given power 
        {
                return alpha_to[power];
        }
GFq_Symbol rssoft::gf::GFq::div ( const GFq_Symbol &  a,
const GFq_Symbol &  b 
) const [inline] 
        {
#if !defined(NO_GFLUT)
                return div_table[a][b];
#else
                if ((a == 0) || (b == 0))
                {
                        return 0;
                }
                else
                {
                        return alpha_to[fast_modulus(index_of[a] - index_of[b] + field_size)];
                }
#endif
        }

Here is the call graph for this function:

GFq_Symbol rssoft::gf::GFq::exp ( const GFq_Symbol &  a,
const int &  n 
) const [inline] 
        {
                if (n == 0)
                {
                        return 1;
                }
                else if (a == 0)
        {
            return 0;
        }
        else
        {
                unsigned int log_a = index_of[a];
                unsigned int log_a_pwr_n = log_a * n;
                return alpha_to[log_a_pwr_n % field_size];
        }
        }
GFq_Symbol rssoft::gf::GFq::fast_modulus ( GFq_Symbol  x) const [private] 
{
        while (x >= (int) field_size)
        {
                x -= (int) field_size;
                x = (x >> power) + (x & (int) field_size);
        }

        return x;
}
GFq_Symbol rssoft::gf::GFq::gen_div ( const GFq_Symbol &  a,
const GFq_Symbol &  b 
) const [private] 
{
        if ((a == 0) || (b == 0))
        {
                return 0;
        }
        else
        {
                return alpha_to[fast_modulus(index_of[a] - index_of[b] + field_size)];
        }
}

Here is the call graph for this function:

GFq_Symbol rssoft::gf::GFq::gen_exp ( const GFq_Symbol &  a,
const unsigned int &  n 
) const [private] 
{
        if (a != 0)
        {
                if (n == 0)
                {
                        return 1;
                }
                else
                {
                        return alpha_to[fast_modulus(index_of[a] * n)];
                }
        }
        else
        {
                return 0;
        }
}

Here is the call graph for this function:

GFq_Symbol rssoft::gf::GFq::gen_inverse ( const GFq_Symbol &  val) const [private] 
{
        return alpha_to[fast_modulus(field_size - index_of[val])];
}

Here is the call graph for this function:

GFq_Symbol rssoft::gf::GFq::gen_mul ( const GFq_Symbol &  a,
const GFq_Symbol &  b 
) const [private] 
{
        if ((a == 0) || (b == 0))
        {
                return 0;
        }
        else
        {
                return alpha_to[fast_modulus(index_of[a] + index_of[b])];
        }
}

Here is the call graph for this function:

void rssoft::gf::GFq::generate_field ( ) [private] 
{
        /*
         Note: It is assumed that the degree of the primitive
         polynomial will be equivelent to the m value as
         in GF(2^m)
         */

        /*
         need to update using stanford method for prim-poly generation.
         */
        int mask = 1;

        alpha_to[power] = 0;

        for (unsigned int i = 0; i < power; i++)
        {
                alpha_to[i] = mask;
                index_of[alpha_to[i]] = i;

                if (primitive_poly[i] != 0)
                {
                        alpha_to[power] ^= mask;
                }

                mask <<= 1;
        }

        index_of[alpha_to[power]] = power;

        mask >>= 1;

        for (unsigned int i = power + 1; i < field_size; i++)
        {
                if (alpha_to[i - 1] >= mask)
                {
                        alpha_to[i] = alpha_to[power] ^ ((alpha_to[i - 1] ^ mask) << 1);
                }
                else
                {
                        alpha_to[i] = alpha_to[i - 1] << 1;
                }

                index_of[alpha_to[i]] = i;
        }

        index_of[0] = GFERROR;
        alpha_to[field_size] = 1;

#if !defined(NO_GFLUT)

        for (unsigned int i = 0; i < field_size + 1; i++)
        {
                for (unsigned int j = 0; j < field_size + 1; j++)
                {
                        mul_table[i][j] = gen_mul(i, j);
                        div_table[i][j] = gen_div(i, j);
                        exp_table[i][j] = gen_exp(i, j);
                }
        }

        for (unsigned int i = 0; i < (field_size + 1); i++)
        {
                mul_inverse[i] = gen_inverse(i);
                mul_inverse[i + (field_size + 1)] = mul_inverse[i];
        }

#endif
}

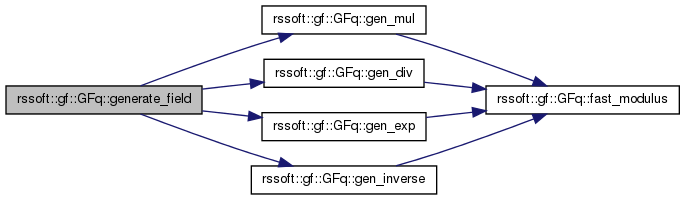
Here is the call graph for this function:

unsigned int rssoft::gf::GFq::index ( const GFq_Symbol  value) const [inline]

Alpha based log

Parameters:
valueSymbol representation of the element
Returns:
The power of alpha corresponding to the element 
        {
                return index_of[value];
        }
GFq_Symbol rssoft::gf::GFq::inverse ( const GFq_Symbol &  val) const [inline] 
        {
#if !defined(NO_GFLUT)
                return mul_inverse[val];
#else
                return alpha_to[fast_modulus(field_size - index_of[val])];
#endif
        }

Here is the call graph for this function:

GFq_Symbol rssoft::gf::GFq::mul ( const GFq_Symbol &  a,
const GFq_Symbol &  b 
) const [inline] 
        {
#if !defined(NO_GFLUT)
                return mul_table[a][b];
#else
                if ((a == 0) || (b == 0))
                {
                        return 0;
                }
                else
                {
                        return alpha_to[fast_modulus(index_of[a] + index_of[b])];
                }
#endif
        }

Here is the call graph for this function:

bool rssoft::gf::GFq::operator!= ( const GFq &  gf) const 
{
        return ((this->power != gf.power) || (this->prim_poly_hash != gf.prim_poly_hash));
}
GFq & rssoft::gf::GFq::operator= ( const GFq &  gf) 
{
        if (this == &gf)
        {
                return *this;
        }

        if (alpha_to != NULL)
        {
                delete[] alpha_to;
        }

        if (index_of != NULL)
        {
                delete[] index_of;
        }

        power = gf.power;
        field_size = gf.field_size;
        prim_poly_hash = gf.prim_poly_hash;

        memcpy(alpha_to, gf.alpha_to, (field_size + 1) * sizeof(GFq_Symbol));
        memcpy(index_of, gf.index_of, (field_size + 1) * sizeof(GFq_Symbol));

#if !defined(NO_GFLUT)

        if (mul_table != NULL)
        {
                delete[] mul_table;
        }

        if (div_table != NULL)
        {
                delete[] div_table;
        }

        if (exp_table != NULL)
        {
                delete[] exp_table;
        }

        if (mul_inverse != NULL)
        {
                delete[] mul_inverse;
        }

        mul_table = new GFq_Symbol*[(field_size + 1)];
        div_table = new GFq_Symbol*[(field_size + 1)];
        exp_table = new GFq_Symbol*[(field_size + 1)];
        mul_inverse = new GFq_Symbol[(field_size + 1) * 2];

        for (unsigned int i = 0; i < (field_size + 1); i++)
        {
                mul_table[i] = new GFq_Symbol[(field_size + 1)];
                div_table[i] = new GFq_Symbol[(field_size + 1)];
                exp_table[i] = new GFq_Symbol[(field_size + 1)];
        }

        memcpy(mul_inverse, gf.mul_inverse, (field_size + 1) * sizeof(GFq_Symbol) * 2);

        memcpy(mul_table, gf.mul_table, (field_size + 1) * sizeof(GFq_Symbol*));
        memcpy(div_table, gf.div_table, (field_size + 1) * sizeof(GFq_Symbol*));
        memcpy(exp_table, gf.exp_table, (field_size + 1) * sizeof(GFq_Symbol*));

        for (unsigned int i = 0; i < (field_size + 1); i++)
        {
                memcpy(mul_table[i], gf.mul_table[i], (field_size + 1) * sizeof(GFq_Symbol));
                memcpy(div_table[i], gf.div_table[i], (field_size + 1) * sizeof(GFq_Symbol));
                memcpy(exp_table[i], gf.exp_table[i], (field_size + 1) * sizeof(GFq_Symbol));
        }

#endif

        return *this;
}
bool rssoft::gf::GFq::operator== ( const GFq &  gf) const 
{
        return ((this->power == gf.power) && (this->prim_poly_hash == gf.prim_poly_hash));
}
unsigned int rssoft::gf::GFq::pwr ( ) const [inline]

Get m the power of 2 in GF(2^m)

Returns:
GF(2^m) exponent 
        {
                return power;
        }
unsigned int rssoft::gf::GFq::size ( ) const [inline]

Get the size of the field

Returns:
The number of elements in the field minus one (i.e. non null elements) 
        {
                return field_size;
        }
GFq_Symbol rssoft::gf::GFq::sub ( const GFq_Symbol &  a,
const GFq_Symbol &  b 
) const [inline] 
        {
                return (a ^ b);
        }

Friends And Related Function Documentation

std::ostream& operator<< ( std::ostream &  os,
const GFq &  gf 
) [friend] 
{
    os << "GF(2^" << gf.pwr() << ")" << std::endl;

    os << "P = " << gf.primitive_poly << std::endl;
    os << "i\ta^i\tlog_a(i)" << std::endl;

    for(unsigned int i = 0; i < gf.field_size + 1; i++)
    {
        os << i << "\t" << gf.alpha_to[i] << "\t" << gf.index_of[i] << std::endl;
    }

    return os;
}

Member Data Documentation

GFq_Symbol* rssoft::gf::GFq::alpha_to [private]

Exponential or anti-log unary operation LUT.

GFq_Symbol** rssoft::gf::GFq::div_table [private]

Division binary operation LUT.

GFq_Symbol** rssoft::gf::GFq::exp_table [private]

Exponent binary operation LUT.

unsigned int rssoft::gf::GFq::field_size [private]

Number of non null elements in the field.

GFq_Symbol* rssoft::gf::GFq::index_of [private]

Log unary operation LUT.

GFq_Symbol* rssoft::gf::GFq::mul_inverse [private]

Multiplicative inverse unary operation LUT.

GFq_Symbol** rssoft::gf::GFq::mul_table [private]

Multiplication binary operation LUT.

unsigned int rssoft::gf::GFq::power [private]

m the power of 2 as in GF(2^m)

unsigned int rssoft::gf::GFq::prim_poly_hash [private]

Primitive polynomial hash coded.

const GF2_Polynomial& rssoft::gf::GFq::primitive_poly [private]

Primitive polynomial.

The documentation for this class was generated from the following files:
 All Classes Namespaces Files Functions Variables Typedefs Friends Defines