rssoft::gf::GFq_BivariatePolynomial Class Reference

Bivariate polynomials with coefficients in GF(2^m) thus the polynomials in GF(2^m)[X,Y]. Division is intentionally omitted as this is complex and unnecessary for the application. More...

#include <GFq_BivariatePolynomial.h>

List of all members.

Public Member Functions
	GFq_BivariatePolynomial (unsigned int w_x, unsigned int w_y)
	GFq_BivariatePolynomial (const std::pair< unsigned int, unsigned int > &_weights)
	GFq_BivariatePolynomial (const GFq_BivariatePolynomial &polynomial)
	~GFq_BivariatePolynomial ()
void	init (std::vector< GFq_BivariateMonomial > &_monomials)
void	init (const GFq_BivariatePolynomial &polynomial)
void	init (const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &monomials)
void	init_x_pow (const GFq &gf, unsigned int x_pow)
void	init_y_pow (const GFq &gf, unsigned int y_pow)
void	init_x_pow_series (const GFq &gf, unsigned int max_pow)
void	init_y_pow_series (const GFq &gf, unsigned int max_pow)
const std::pair< unsigned int, unsigned int > &	get_weights () const
bool	is_valid () const
bool	is_const (GFq_Element &const_value) const
bool	is_zero () const
bool	is_one () const
const std::map < GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	get_monomials () const
std::map < GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	get_monomials_for_update ()
GFq_BivariateMonomial	get_leading_monomial () const
unsigned int	lmX () const
unsigned int	lmY () const
unsigned int	wdeg () const
GFq_BivariatePolynomial &	operator= (const GFq_BivariatePolynomial &polynomial)
GFq_BivariatePolynomial &	operator+= (const GFq_BivariatePolynomial &polynomial)
GFq_BivariatePolynomial &	operator+= (const GFq_Element &gfe)
GFq_BivariatePolynomial &	operator-= (const GFq_BivariatePolynomial &polynomial)
GFq_BivariatePolynomial &	operator-= (const GFq_Element &gfe)
GFq_BivariatePolynomial &	operator*= (const GFq_BivariatePolynomial &polynomial)
GFq_BivariatePolynomial &	operator*= (const GFq_BivariateMonomial &monomial)
GFq_BivariatePolynomial &	operator*= (const GFq_Element &gfe)
GFq_BivariatePolynomial &	operator/= (const GFq_BivariateMonomial &monomial)
GFq_BivariatePolynomial &	operator/= (const GFq_Element &gfe)
GFq_BivariatePolynomial &	operator^= (unsigned int n)
bool	operator== (const GFq_BivariatePolynomial &polynomial) const
bool	operator!= (const GFq_BivariatePolynomial &polynomial) const
GFq_Element	operator() (const GFq_Element &x_value, const GFq_Element &y_value) const
GFq_BivariatePolynomial	operator() (const GFq_BivariatePolynomial &P, const GFq_BivariatePolynomial &Q) const
GFq_Polynomial	get_X_0 () const
GFq_Polynomial	get_0_Y () const
bool	is_in_X () const
bool	is_in_Y () const
GFq_BivariatePolynomial &	make_star ()
GFq_BivariatePolynomial &	make_dHasse (unsigned int mu, unsigned int nu)
Static Public Member Functions
static void	sum (std::vector< GFq_BivariateMonomial > &sum_monomials, const GFq_BivariatePolynomial &a, const GFq_BivariatePolynomial &b)
static void	product (std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &prod_monomials, const GFq_BivariatePolynomial &a, const GFq_BivariatePolynomial &b)
static void	division (std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &div_monomials, const GFq_BivariatePolynomial &a, const GFq_BivariateMonomial &b)
static void	pow (std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &pow_monomials, const GFq_BivariatePolynomial &a, unsigned int n)
static void	simplify (std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &monomials)
Protected Member Functions
GFq_Polynomial	get_v_0 (bool x_terms) const
bool	is_in_v (bool x_terms) const
Static Protected Member Functions
static void	product (std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &prod_monomials, const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &a_monomials, const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &b_monomials)
static void	product (std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &prod_monomials, const GFq_Element &v, const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &a_monomials, const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &b_monomials)
static void	add_monomial (std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &monomials, const GFq_BivariateMonomialKeyValueRepresentation &a)
static void	add_monomial (std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &monomials, const GFq_Element &coeff, unsigned int x_pow, unsigned int y_pow)
Protected Attributes
std::pair< unsigned int, unsigned int >	weights
std::map < GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial >	monomials
Friends
std::ostream &	operator<< (std::ostream &os, const GFq_BivariatePolynomial &polynomial)

---

Detailed Description

Bivariate polynomials with coefficients in GF(2^m) thus the polynomials in GF(2^m)[X,Y]. Division is intentionally omitted as this is complex and unnecessary for the application.

---

Constructor & Destructor Documentation

rssoft::gf::GFq_BivariatePolynomial::GFq_BivariatePolynomial	(	unsigned int	w_x,
		unsigned int	w_y
	)

Constructs a new empty (thus invalid) bivariate polynomial

Parameters:

w_x	Weight in X for monomials weighted ordering
w_y	Weight in Y for monomials weighted ordering

                                                                                   :
                weights(w_x,w_y),
                monomials(GFq_WeightedRevLex_BivariateMonomial(w_x,w_y))
{}

rssoft::gf::GFq_BivariatePolynomial::GFq_BivariatePolynomial

(

const std::pair< unsigned int, unsigned int > &

_weights

)

Constructs a new empty (thus invalid) bivariate polynomial

Parameters:

weights

Weight in X,Y pair for monomials weighted ordering

                                                                                                    :
        weights(_weights),
        monomials(GFq_WeightedRevLex_BivariateMonomial(_weights))
{}

rssoft::gf::GFq_BivariatePolynomial::GFq_BivariatePolynomial

(

const GFq_BivariatePolynomial &

polynomial

)

Copy constructor.

Parameters:

polynomial

Polynomial to copy from

                                                                                          :
                weights(polynomial.get_weights()),
                monomials(GFq_WeightedRevLex_BivariateMonomial(polynomial.get_weights()))
{
    monomials = polynomial.monomials;
}

rssoft::gf::GFq_BivariatePolynomial::~GFq_BivariatePolynomial

(

)

Destructor

{}

---

Member Function Documentation

void rssoft::gf::GFq_BivariatePolynomial::add_monomial	(	std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	monomials,
		const GFq_BivariateMonomialKeyValueRepresentation &	a
	)		[static, protected]

Helper method to add a monomial to a map of monomials

{
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::iterator mono_it = monomials.find(a.first);

        if (mono_it == monomials.end()) // exponents pair does not exist yet
        {
                monomials.insert(a); // insert the new monomial
        }
        else // exponents pair already exist
        {
                mono_it->second += a.second; // add coefficients
        }
}

void rssoft::gf::GFq_BivariatePolynomial::add_monomial	(	std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	monomials,
		const GFq_Element &	coeff,
		unsigned int	x_pow,
		unsigned int	y_pow
	)		[static, protected]

Helper method to add a monomial to a map of monomials

{
        GFq_BivariateMonomialExponents exponents(x_pow, y_pow);
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::iterator mono_it = monomials.find(exponents);

        if (mono_it == monomials.end()) // exponents pair does not exist yet
        {
                GFq_BivariateMonomialKeyValueRepresentation a(exponents, coeff);
                monomials.insert(a); // insert the new monomial
        }
        else // exponents pair already exist
        {
                mono_it->second += coeff; // add coefficients
        }
}

void rssoft::gf::GFq_BivariatePolynomial::division	(	std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	div_monomials,
		const GFq_BivariatePolynomial &	a,
		const GFq_BivariateMonomial &	b
	)		[static]

Helper method to create the map of monomials of the division of polynomial a by monomial b

{
        const std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>& a_monomials = a.get_monomials();
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator a_it = a_monomials.begin();

        for (; a_it != a_monomials.end(); ++a_it)
        {
                GFq_BivariateMonomial mono_div = static_cast<GFq_BivariateMonomial>(*a_it) / b;
                div_monomials.insert(mono_div);
        }
}

Here is the call graph for this function:

GFq_Polynomial rssoft::gf::GFq_BivariatePolynomial::get_0_Y

(

)

const

Evaluation of polynomial for X=0 as a univariate polynomial in Y

Returns:

Univariate polynomial in Y as P(0,Y)

{
        return get_v_0(false);
}

Here is the call graph for this function:

GFq_BivariateMonomial rssoft::gf::GFq_BivariatePolynomial::get_leading_monomial

(

)

const [inline]

Get a copy of the leading monomial with respect to weighted reverse lexical order

Returns:

Reference to the leading monomial

        {
                return static_cast<GFq_BivariateMonomial>(*(monomials.rbegin()));
        }

const std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>& rssoft::gf::GFq_BivariatePolynomial::get_monomials

(

)

const [inline]

Get the monomials

Returns:

Reference to the set of monomials

        {
                return monomials;
        }

std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>& rssoft::gf::GFq_BivariatePolynomial::get_monomials_for_update

(

)

[inline]

Get the monomials to be updated

Returns:

Reference to the set of monomials

        {
                return monomials;
        }

GFq_Polynomial rssoft::gf::GFq_BivariatePolynomial::get_v_0

(

bool

x_terms

)

const [protected]

{
        if (monomials.size() == 0)
        {
                throw GF_Exception("Bivariate polynomial is invalid");
        }
        else
        {
                std::map<unsigned int, GFq_Element> poly_map;
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator mono_it = monomials.begin();
                const GFq& gf = mono_it->second.field();
                GFq_Element zero(gf,0);

                for (; mono_it != monomials.end(); ++mono_it)
                {
                        if (x_terms)
                        {
                                if (mono_it->first.second == 0) // no Y term
                                {
                                        poly_map.insert(std::make_pair(mono_it->first.first, mono_it->second));
                                }
                        }
                        else
                        {
                                if (mono_it->first.first == 0) // no X term
                                {
                                        poly_map.insert(std::make_pair(mono_it->first.second, mono_it->second));
                                }
                        }
                }

                if (poly_map.size() == 0)
                {
                        return GFq_Polynomial(zero);
                }
                else
                {
                        unsigned int max_pow = poly_map.rbegin()->first;
                        std::vector<GFq_Element> poly(max_pow+1, zero);
                        std::map<unsigned int, GFq_Element>::const_iterator x_map_it = poly_map.begin();

                        for (; x_map_it != poly_map.end(); ++x_map_it)
                        {
                                poly[x_map_it->first] = x_map_it->second;
                        }

                        return GFq_Polynomial(gf, poly);
                }
        }
}

const std::pair<unsigned int, unsigned int>& rssoft::gf::GFq_BivariatePolynomial::get_weights

(

)

const [inline]

Gets the weights pair in (X,Y) used for weighted monomial ordering

Returns:

Reference to the weights pair in (X,Y) used for weighted monomial ordering

        {
                return weights;
        }

GFq_Polynomial rssoft::gf::GFq_BivariatePolynomial::get_X_0

(

)

const

Evaluation of polynomial for Y=0 as a univariate polynomial in X

Returns:

Univariate polynomial in X as P(X,0)

{
        return get_v_0(true);
}

Here is the call graph for this function:

void rssoft::gf::GFq_BivariatePolynomial::init

(

std::vector< GFq_BivariateMonomial > &

_monomials

)

Initializes the polynomial as a sum of monomials

Parameters:

monomials

List of monomials

{
        monomials.clear();
        monomials.insert(_monomials.begin(), _monomials.end());
}

void rssoft::gf::GFq_BivariatePolynomial::init

(

const GFq_BivariatePolynomial &

polynomial

)

Initializes the polynomial with the monomials of another polynomial

{
    monomials = polynomial.monomials;
}

void rssoft::gf::GFq_BivariatePolynomial::init

(

const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &

monomials

)

Initializes the polynomial with a map of monomials

{
        monomials = _monomials;
}

void rssoft::gf::GFq_BivariatePolynomial::init_x_pow	(	const GFq &	gf,
		unsigned int	x_pow
	)

Initializes the polynomial as X^n

Parameters:

gf	Galois Field to create the unit GF element as coefficient
max_pow	power of polynomial's unique monomial

{
    monomials.insert(std::make_pair(std::make_pair(x_pow,0), GFq_Element(gf, 1)));
}

void rssoft::gf::GFq_BivariatePolynomial::init_x_pow_series	(	const GFq &	gf,
		unsigned int	max_pow
	)

Initializes the polynomial as 1+X+..+X^n

Parameters:

gf	Galois Field to create the unit GF element as coefficient
max_pow	Maximum power in the series

{
    for (unsigned int i = 0; i <= max_pow; i++)
    {
        monomials.insert(std::make_pair(std::make_pair(i,0), GFq_Element(gf, 1)));
    }
}

void rssoft::gf::GFq_BivariatePolynomial::init_y_pow	(	const GFq &	gf,
		unsigned int	y_pow
	)

Initializes the polynomial as Y^n

Parameters:

gf	Galois Field to create the unit GF element as coefficient
max_pow	power of polynomial's unique monomial

{
    monomials.insert(std::make_pair(std::make_pair(0, y_pow), GFq_Element(gf, 1)));
}

void rssoft::gf::GFq_BivariatePolynomial::init_y_pow_series	(	const GFq &	gf,
		unsigned int	max_pow
	)

Initializes the polynomial as 1+Y+..+Y^n

Parameters:

gf	Galois Field to create the unit GF element as coefficient
max_pow	Maximum power in the series

{
    for (unsigned int i = 0; i <= max_pow; i++)
    {
        monomials.insert(std::make_pair(std::make_pair(0,i), GFq_Element(gf, 1)));
    }
}

bool rssoft::gf::GFq_BivariatePolynomial::is_const

(

GFq_Element &

const_value

)

const

Tells if the polynomial has only one constant coefficient with the given value

{
        if (monomials.size() == 1)
        {
                const GFq_BivariateMonomialKeyValueRepresentation& m0 = *(monomials.begin());

                if (m0.second == const_value)
                {
                        return (m0.first.are_zero());
                }
                else
                {
                        return false;
                }
        }
        else
        {
                return false;
        }
}

bool rssoft::gf::GFq_BivariatePolynomial::is_in_v

(

bool

x_terms

)

const [protected]

{
        if (monomials.size() == 0)
        {
                throw GF_Exception("Bivariate polynomial is invalid");
        }
        else
        {
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator mono_it = monomials.begin();
        
        for (; mono_it != monomials.end(); ++mono_it)
        {
            if (x_terms)
            {
                if (mono_it->first.second != 0)
                {
                    return false;
                }
            }
            else
            {
                if (mono_it->first.first != 0)
                {
                    return false;
                }
            }
        }
        
        return true;
    }
}

bool rssoft::gf::GFq_BivariatePolynomial::is_in_X

(

)

const

Tells if a polynomial has only terms in X

{
    return is_in_v(true);
}

Here is the call graph for this function:

bool rssoft::gf::GFq_BivariatePolynomial::is_in_Y

(

)

const

Tells if a polynomial has only terms in Y

{
    return is_in_v(false);
}

Here is the call graph for this function:

bool rssoft::gf::GFq_BivariatePolynomial::is_one

(

)

const

Tells if the polynomial is P(X)=1

{
        if (monomials.size() == 0)
        {
                return true;
        }
        else
        {
                if (monomials.size() == 1)
                {
                        const GFq_BivariateMonomialKeyValueRepresentation& m0 = *(monomials.begin());

                        if (m0.second.is_one())
                        {
                                return (m0.first.are_zero());
                        }
                        else
                        {
                                return false;
                        }
                }
                else
                {
                        return false;
                }
        }
}

bool rssoft::gf::GFq_BivariatePolynomial::is_valid

(

)

const

Tells if the polynomial has coefficients

{
        return monomials.size() != 0;
}

bool rssoft::gf::GFq_BivariatePolynomial::is_zero

(

)

const

Tells if the polynomial has no coefficients or a null coefficient

{
        if (monomials.size() == 0)
        {
                return true;
        }
        else
        {
                if (monomials.size() == 1)
                {
                        const GFq_BivariateMonomialKeyValueRepresentation& m0 = *(monomials.begin());

                        if (m0.second.is_zero())
                        {
                                return (m0.first.are_zero());
                        }
                        else
                        {
                                return false;
                        }
                }
                else
                {
                        return false;
                }
        }
}

unsigned int rssoft::gf::GFq_BivariatePolynomial::lmX

(

)

const [inline]

Get X power of leading monomial

    {
        return static_cast<GFq_BivariateMonomial>(*(monomials.rbegin())).eX();
    }

Here is the call graph for this function:

unsigned int rssoft::gf::GFq_BivariatePolynomial::lmY

(

)

const [inline]

Get Y power of leading monomial

    {
        return static_cast<GFq_BivariateMonomial>(*(monomials.rbegin())).eY();
    }

Here is the call graph for this function:

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::make_dHasse	(	unsigned int	mu,
		unsigned int	nu
	)

Applies to self the [mu,nu] Hasse derivative

Parameters:

mu	mu parameter (applies to X factors)
nu	nu parameter (applies to Y factors)

Returns:

reference to the new polynomial

{
        if (monomials.size() == 0)
        {
                throw GF_Exception("Bivariate polynomial is invalid");
        }
        else if ((mu != 0) or (nu != 0)) // ^[0,0] is the trivial case where the polynomial is unmodified
        {
                GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(weights);
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> hasse_monomials(mono_exp_compare);
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator mono_it = monomials.begin();
                const GFq& gf = mono_it->second.field();

                for (; mono_it != monomials.end(); ++mono_it)
                {
                        unsigned int eX = mono_it->first.first;
                        unsigned int eY = mono_it->first.second;

                        if (!(eX < mu) && !(eY < nu))
                        {
                                // coefficient is not null if both binomial coefficients are even
                                if (!(binomial_coeff_parity(eX,mu)) && !(binomial_coeff_parity(eY,nu)))
                                {
                                        hasse_monomials.insert(std::make_pair(std::make_pair(eX-mu, eY-nu), mono_it->second));
                                }
                        }
                }

                if (hasse_monomials.size() == 0)
                {
                        monomials.clear();
                        monomials.insert(std::make_pair(std::make_pair(0,0), GFq_Element(gf, 0)));
                }
                else
                {
                        monomials = hasse_monomials;
                }
        }

        return *this;
}

Here is the call graph for this function:

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::make_star

(

)

Applies to self the star function as P*(X,Y) = P(X,Y)/X^h where h is the greatest power of X so that X^h divides P

Returns:

reference to the new polynomial

{
        if (monomials.size() == 0)
        {
                throw GF_Exception("Bivariate polynomial is invalid");
        }
        else
        {
                std::set<unsigned int> x_exp_set;
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator mono_it = monomials.begin();
                const GFq& gf = mono_it->second.field();
                
                for (; mono_it != monomials.end(); ++mono_it)
                {
                        x_exp_set.insert(mono_it->first.first);
                }
                
                unsigned int h = *(x_exp_set.begin());
                
                if (h > 0)
                {
                        GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(weights);
                        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> div_monomials(mono_exp_compare);
                        mono_it = monomials.begin();
                        
                        for (; mono_it != monomials.end(); ++mono_it)
                        {
                                div_monomials.insert(std::make_pair(std::make_pair(mono_it->first.first-h, mono_it->first.second), mono_it->second));
                        }
                        
                        monomials = div_monomials;
                }
        }
        
        return *this;
}

bool rssoft::gf::GFq_BivariatePolynomial::operator!=

(

const GFq_BivariatePolynomial &

polynomial

)

const

{
        return (weights != polynomial.weights) || (monomials != polynomial.monomials);
}

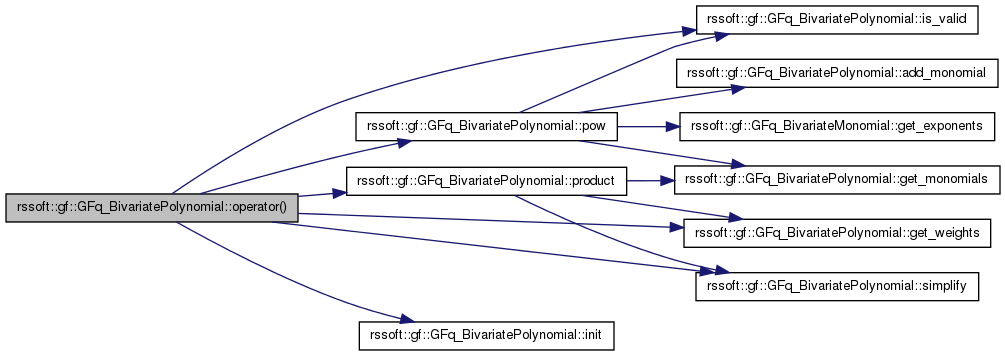
GFq_Element rssoft::gf::GFq_BivariatePolynomial::operator()	(	const GFq_Element &	x_value,
		const GFq_Element &	y_value
	)		const

Evaluation of bivariate polynomial at a (x,y) point in GFq^2

Parameters:

x_value	x coordinate
y_value	y coordinate

Returns:

Value of polynomial at (x,y) point

{
        if (x_value.field() != y_value.field())
        {
                throw GF_Exception("point coordinates must be of the same Galois Field to evaluate bivariate polynomial at this point");
        }
        else
        {
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator mono_it = monomials.begin();
                GFq_Element result(mono_it->second.field(), 0);

                for (; mono_it != monomials.end(); ++mono_it)
                {
                        result += (x_value^mono_it->first.first) * (y_value^mono_it->first.second) * (mono_it->second);
                }

                return result;
        }
}

Here is the call graph for this function:

GFq_BivariatePolynomial rssoft::gf::GFq_BivariatePolynomial::operator()	(	const GFq_BivariatePolynomial &	P,
		const GFq_BivariatePolynomial &	Q
	)		const

Evaluation of bivariate polynomial at (P(X,Y),Q(X,Y))

Parameters:

P	Polynomial in place of X
Q	Polynomial in place of Y

Returns:

(*this)(P(X,Y),Q(X,Y))

{
        if (monomials.size() == 0)
        {
                throw GF_Exception("Bivariate polynomial is invalid");
        }
        else if (!P.is_valid())
        {
                throw GF_Exception("First operand polynomial is invalid");
        }
        else if (!Q.is_valid())
        {
                throw GF_Exception("Second operand polynomial is invalid");
        }
        else if (P.get_weights() != Q.get_weights())
        {
                throw GF_Exception("Cannot evaluate with polynomials of different weights");
        }
        else
        {
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator mono_it = monomials.begin();
                const GFq& gf = mono_it->second.field();
                GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(weights); // Use reverse lexical order
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> result_monomials(mono_exp_compare);

                for (; mono_it != monomials.end(); ++mono_it)
                {
                        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> partX_monomials(mono_exp_compare);
                        pow(partX_monomials, P, mono_it->first.first); // X^i -> (P(X,Y))^i
                        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> partY_monomials(mono_exp_compare);
                        pow(partY_monomials, Q, mono_it->first.second); // Y^j -> (Q(X,Y))^j
                        product(result_monomials, mono_it->second, partX_monomials, partY_monomials); // a_i,j*(P(X,Y))^i*(Q(X,Y))^j
                }

                simplify(result_monomials); // simplify the resulting monomials (removes those with zero coefficient)
                GFq_BivariatePolynomial result(weights);
                result.init(result_monomials);
                return result;
        }
}

Here is the call graph for this function:

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator*=

(

const GFq_BivariatePolynomial &

polynomial

)

{
        GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(weights);
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> product_monomials(mono_exp_compare);

        product(product_monomials, *this, polynomial);
        monomials = product_monomials;

        return *this;
}

Here is the call graph for this function:

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator*=

(

const GFq_BivariateMonomial &

monomial

)

{
        GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(weights);
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> product_monomials(mono_exp_compare);
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator mono_it = monomials.begin();
        
        for (; mono_it != monomials.end(); ++mono_it)
        {
                unsigned int eX = mono_it->first.first + monomial.eX();
                unsigned int eY = mono_it->first.second + monomial.eY();
                product_monomials.insert(std::make_pair(std::make_pair(eX, eY), mono_it->second * monomial.coeff()));
        }
        
        monomials = product_monomials;
        
        return *this;
}

Here is the call graph for this function:

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator*=

(

const GFq_Element &

gfe

)

{
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::iterator mono_it = monomials.begin();

        for (; mono_it != monomials.end(); ++mono_it)
        {
                mono_it->second *= gfe;
        }

        return *this;
}

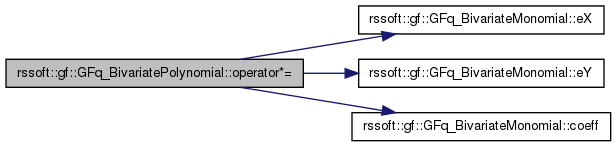
GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator+=

(

const GFq_BivariatePolynomial &

polynomial

)

{
        std::vector<GFq_BivariateMonomial> sum_monomials;

        sum(sum_monomials, *this, polynomial);

        monomials.clear();
        monomials.insert(sum_monomials.begin(), sum_monomials.end());

        return *this;
}

Here is the call graph for this function:

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator+=

(

const GFq_Element &

gfe

)

{
        if (monomials.size() == 0)
        {
                monomials.insert(std::make_pair(std::make_pair(0,0), gfe));
        }
        else
        {
                if (monomials.begin()->first.are_zero()) // constant monomial
                {
                        monomials.begin()->second += gfe;
                }
                else
                {
                        monomials.insert(std::make_pair(std::make_pair(0,0), gfe));
                }
        }

        return *this;
}

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator-=

(

const GFq_BivariatePolynomial &

polynomial

)

{
        return (*this += polynomial);
}

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator-=

(

const GFq_Element &

gfe

)

{
        return (*this += gfe);
}

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator/=

(

const GFq_BivariateMonomial &

monomial

)

{
        GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(weights);
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> div_monomials(mono_exp_compare);

        division(div_monomials, *this, monomial);
        monomials = div_monomials;

        return *this;
}

Here is the call graph for this function:

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator/=

(

const GFq_Element &

gfe

)

{
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::iterator mono_it = monomials.begin();

        for (; mono_it != monomials.end(); ++mono_it)
        {
                mono_it->second /= gfe;
        }

        return *this;
}

GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator=

(

const GFq_BivariatePolynomial &

polynomial

)

{
        weights = polynomial.weights;
        monomials = polynomial.monomials;
        return *this;
}

bool rssoft::gf::GFq_BivariatePolynomial::operator==

(

const GFq_BivariatePolynomial &

polynomial

)

const

{
        return (weights == polynomial.weights) && (monomials == polynomial.monomials);
}

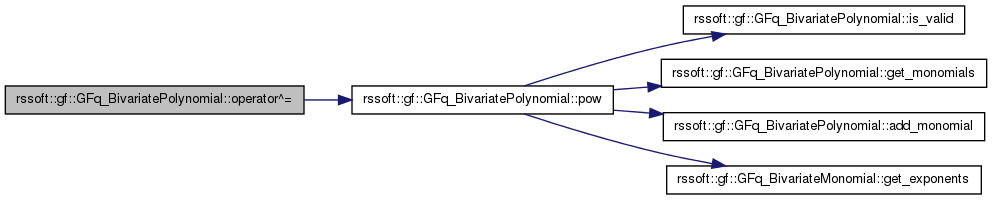
GFq_BivariatePolynomial & rssoft::gf::GFq_BivariatePolynomial::operator^=

(

unsigned int

n

)

{
        GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(weights);
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> pow_monomials(mono_exp_compare);

        pow(pow_monomials, *this, n);
        monomials = pow_monomials;

        return *this;
}

Here is the call graph for this function:

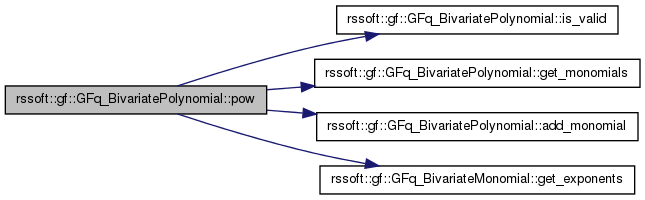
void rssoft::gf::GFq_BivariatePolynomial::pow	(	std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	pow_monomials,
		const GFq_BivariatePolynomial &	a,
		unsigned int	n
	)		[static]

Helper method to create the map of monomials of the polynomial to the nth power

< temporary a^i monomials

< temporary power monomials

{
        if (!a.is_valid())
        {
                throw GF_Exception("Invalid polynomial");
        }
        else
        {
                const std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>& a_monomials = a.get_monomials();
                const GFq& gf = a_monomials.begin()->second.field();

                if (n == 0)
                {
                        pow_monomials.insert(std::make_pair(std::make_pair(0,0), GFq_Element(gf,1))); // P^n = 1
                }
                else if (n == 1) // P^1 = P
                {
                        pow_monomials = a_monomials;
                }
                else if (a_monomials.size() == 1) // Optimization if polynomial is reduced to a single monomial: (a*X^i*Y^j)^n = a^n*X^(i*n)*Y^(j*n)
        {
            add_monomial(pow_monomials, (a_monomials.begin()->second)^n, (a_monomials.begin()->first.first)*n, (a_monomials.begin()->first.second)*n);
        }
        else
                {
                        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> at_monomials(a_monomials); 
                        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> pt_monomials(pow_monomials); 

                        for (unsigned int i=0; i<n-1; i++)
                        {
                                pt_monomials.clear();

                                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator at_it = at_monomials.begin();
                                for (; at_it != at_monomials.end(); ++at_it)
                                {
                                        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator a_it = a_monomials.begin();
                                        for (; a_it != a_monomials.end(); ++a_it)
                                        {
                                                GFq_BivariateMonomial mono_product = static_cast<GFq_BivariateMonomial>(*at_it) * static_cast<GFq_BivariateMonomial>(*a_it);
                                                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::iterator mono_it = pt_monomials.find(mono_product.get_exponents());

                                                if (mono_it == pt_monomials.end()) // exponents pair does not exist yet
                                                {
                                                        pt_monomials.insert(mono_product); // insert the new monomial
                                                }
                                                else // exponents pair already exist
                                                {
                                                        mono_it->second += mono_product.second; // add coefficients
                                                }
                                        }
                                }

                                at_monomials = pt_monomials;
                        }

                        // copy last temporary a^i monomials to result and simplify

                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::iterator mono_it = at_monomials.begin();

                for (; mono_it != at_monomials.end(); ++mono_it)
                {
                    if (!mono_it->second.is_zero())
                    {
                        add_monomial(pow_monomials, *mono_it);
                    }
                }
                }
        }
}

Here is the call graph for this function:

void rssoft::gf::GFq_BivariatePolynomial::product	(	std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	prod_monomials,
		const GFq_BivariatePolynomial &	a,
		const GFq_BivariatePolynomial &	b
	)		[static]

Helper method to create the map of monomials of the product of polynomials a and b

{
        if (a.get_weights() != b.get_weights())
        {
                throw GF_Exception("Cannot add bivariate polynomials with different degree weights");
        }
        else
        {
                product(prod_monomials, a.get_monomials(), b.get_monomials());
                simplify(prod_monomials); // simplify (removes monomials with zero coefficients)
        }
}

Here is the call graph for this function:

void rssoft::gf::GFq_BivariatePolynomial::product	(	std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	prod_monomials,
		const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	a_monomials,
		const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	b_monomials
	)		[static, protected]

Helper method to create the map of monomials of the product of maps a and b

{
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator a_it = a_monomials.begin();

        for (; a_it != a_monomials.end(); ++a_it)
        {
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator b_it = b_monomials.begin();

                for (; b_it != b_monomials.end(); ++b_it)
                {
                        GFq_BivariateMonomial mono_product = static_cast<GFq_BivariateMonomial>(*a_it) * static_cast<GFq_BivariateMonomial>(*b_it);
                        add_monomial(prod_monomials, mono_product);
                }
        }
}

Here is the call graph for this function:

void rssoft::gf::GFq_BivariatePolynomial::product	(	std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	prod_monomials,
		const GFq_Element &	v,
		const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	a_monomials,
		const std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &	b_monomials
	)		[static, protected]

Helper method to create the map of monomials of the product of constant, maps a and b

{
        std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator a_it = a_monomials.begin();

        for (; a_it != a_monomials.end(); ++a_it)
        {
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator b_it = b_monomials.begin();

                for (; b_it != b_monomials.end(); ++b_it)
                {
                        GFq_BivariateMonomial mono_product = v * static_cast<GFq_BivariateMonomial>(*a_it) * static_cast<GFq_BivariateMonomial>(*b_it);
                        add_monomial(prod_monomials, mono_product);
                }
        }
}

Here is the call graph for this function:

void rssoft::gf::GFq_BivariatePolynomial::simplify

(

std::map< GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial > &

monomials

)

[static]

Helper method to simplify a map of monomials i.e. remove those with coefficient 0

{
    std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::iterator mono_it = monomials.begin();

    while (mono_it != monomials.end())
    {
        if (mono_it->second.is_zero())
        {
                monomials.erase(mono_it++);
        }
        else
        {
                ++mono_it;
        }
    }
}

void rssoft::gf::GFq_BivariatePolynomial::sum	(	std::vector< GFq_BivariateMonomial > &	sum_monomials,
		const GFq_BivariatePolynomial &	a,
		const GFq_BivariatePolynomial &	b
	)		[static]

Helper method to create the vector of monomials of the sum of polynomials a and b

{
        if (a.get_weights() != b.get_weights())
        {
                throw GF_Exception("Cannot add bivariate polynomials with different degree weights");
        }
        else
        {
                std::vector<GFq_BivariateMonomial> sum_monomials;
                GFq_WeightedRevLex_BivariateMonomial mono_exp_compare(a.get_weights()); // Use reverse lexical order
                const std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>& a_monomials = a.get_monomials();
                const std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>& b_monomials = b.get_monomials();
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator a_it = a_monomials.begin();
                std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator b_it = b_monomials.begin();

                while ((a_it != a_monomials.end()) || (b_it != b_monomials.end()))
                {
                        if (a_it == a_monomials.end())
                        {
                                sum_monomials.push_back(static_cast<GFq_BivariateMonomial>(*b_it));
                                ++b_it;
                        }
                        else if (b_it ==  b_monomials.end())
                        {
                                sum_monomials.push_back(static_cast<GFq_BivariateMonomial>(*a_it));
                                ++a_it;
                        }
                        else
                        {
                                if (mono_exp_compare(a_it->first, b_it->first)) // a monomial is less than b
                                {
                                        sum_monomials.push_back(static_cast<GFq_BivariateMonomial>(*a_it));
                                        ++a_it;
                                }
                                else if (mono_exp_compare(b_it->first, a_it->first)) // b monomial is less than a
                                {
                                        sum_monomials.push_back(static_cast<GFq_BivariateMonomial>(*b_it));
                                        ++b_it;
                                }
                                else // monomial orders are equal (thus their exponents are equal) so coefficient can be summed up
                                {
                                        sum_monomials.push_back(static_cast<GFq_BivariateMonomial>(*a_it));
                                        sum_monomials.back().second += b_it->second;
                                        ++a_it;
                                        ++b_it;
                                }
                        }
                }

        // simplify (removes monomials with zero coefficients)

                std::vector<GFq_BivariateMonomial>::iterator mono_it = sum_monomials.begin();

        for (; mono_it != sum_monomials.end(); ++mono_it)
        {
            if (!(mono_it->second.is_zero()))
            {
                _sum_monomials.push_back(*mono_it);
            }
        }

        }
}

Here is the call graph for this function:

unsigned int rssoft::gf::GFq_BivariatePolynomial::wdeg

(

)

const

Weighted degree of polynomial. That is the highest weighted degree of its monomials.

{
    std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial>::const_iterator mono_it = monomials.begin();
    unsigned int max_wd = 0;
    
    for (; mono_it != monomials.end(); ++mono_it)
    {
        GFq_BivariateMonomial mono = static_cast<GFq_BivariateMonomial>(*mono_it);
        
        if (mono.wdeg(weights) > max_wd)
        {
            max_wd = mono.wdeg(weights);
        }
    }
    
    return max_wd;
}

Here is the call graph for this function:

---

Friends And Related Function Documentation

std::ostream& operator<<	(	std::ostream &	os,
		const GFq_BivariatePolynomial &	polynomial
	)		[friend]

Prints a polynomial to an output stream

{
        if (polynomial.monomials.size() == 0)
        {
                os << "<invalid>";
        }
        else
        {
                std::map<GFq_BivariateMonomialExponents, GFq_Element>::const_iterator it = polynomial.monomials.begin();

                for (; it != polynomial.monomials.end(); ++it)
                {
                        if (it != polynomial.monomials.begin())
                        {
                                os << " + ";
                        }

                        os << *it;
                }
        }

        return os;
}

---

Member Data Documentation

std::map<GFq_BivariateMonomialExponents, GFq_Element, GFq_WeightedRevLex_BivariateMonomial> rssoft::gf::GFq_BivariatePolynomial::monomials [protected]

std::pair<unsigned int, unsigned int> rssoft::gf::GFq_BivariatePolynomial::weights [protected]

---

The documentation for this class was generated from the following files:

• /shared/development/google_code/rssoft/library/lib/GFq_BivariatePolynomial.h
• /shared/development/google_code/rssoft/library/lib/GFq_BivariatePolynomial.cpp